立体几何与空间向量
共2637题

立体几何与空间向量
共2637题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

14．某几何体的三视图如图所示，则该几何体的表面积为__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

18.如图，ABCD是边长为2的正方形，平面ABCD，平面ABCD，DE=2AF，BE与平面ABCD所成角为45°．

（Ⅰ）求证：平面BDF；

（Ⅱ）求证：AC//平面BEF；

（Ⅲ）求几何体EFABCD的体积．

正确答案

解：

（I）证明：∵平面ABCD，平面ABCD，∴．

∵ABCD是正方形，∴，∴平面BDE．

（II）证明：延长DA，EF相交于点M，连接BM，

∵平面ABCD，平面ABCD，∴AF//DE，

又DE=2AF，∴AM=AD=2，

∵AD BC，∴AM BC，四边形AMBC为平行四边形，

∴AC//MB，

又MB 平面BEF，AC平面BEF，

∴AC//平面BEF．

（III）由（II）可知几何体EFABCD的体积等于四棱锥的体积减去四棱锥的体积．

∵，四边形MBCD为直角梯形，

平面ABCD，平面ABCD，DE=2AF，AF=，DE=，

所以几何体EFABCD的体积为

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

5．如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的表面积为（）

正确答案

解析

直观图如图所示四棱锥，，

，，

故此棱锥的表面积为，故选A.

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

20．已知椭圆的中心在坐标原点，右焦点为，、是椭圆的左、右顶点，是椭圆上异于、的动点，且面积的最大值为．

（1）求椭圆的方程；

（2）是否存在一定点（），使得当过点的直线与曲线相交于，两点时，为定值？若存在，求出定点和定值；若不存在，请说明理由.

正确答案

解：

（1）设椭圆的方程为（），由已知可得①，∵为椭圆右焦点，∴②，

由①②可得，，

椭圆的方程为；

（2）过点取两条分别垂直于轴和轴的弦，，

则，即，

解得，∴若存在必为，定值为3，

下证满足题意，

设过点的直线方程为，代入中得：，设，，则，，

，综上得定点为，定值为3.

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

填空题 · 5 分

12．已知，，若，，且，则________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

8．若的三个顶点及平面内一点满足，且实数满足：，则实数的值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

3．设与垂直，则的值等于（）

D-l

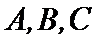
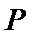
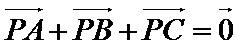
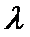
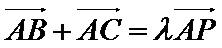
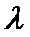
正确答案

解析

由题意得：所以因此选B.

知识点

空间几何体的结构特征

题型：填空题

填空题 · 5 分

11．如下图，某几何体的三视图均为边长为的正方形，则该几何体的体积是_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

18．如图，在四棱锥中底面，底面是直角梯形，为侧棱上一点．该四棱锥的俯视图与侧（左）视图如图所示。

（I）证明：平面；

（II）证明：平面；

（III）求四棱锥的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

填空题 · 5 分

15．已知某几何体的三视图如图，则该几何体的表面积为_________.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

18．已知向量，设函数＋

（1）若，f（x）=，求的值；

（2）在△ABC中，角A，B，C的对边分别是，且满足，求f（B）的取值范围。

正确答案

（1）依题意得，

由

得：，

，

从而可得，

则

（2）由

得：，

从而，

故f（B）=sin（）

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

简答题 · 12 分

19．在多面体ABCDEF中，点O是矩形ABCD的对角线的交点，平面CDE是等边三角形，棱EF//BC且EF=。

（I）证明：FO∥平面CDE；

（II）设BC=是否存在实数，使EO⊥平面CDF，若不存在请说明理由；若存在，试求出的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

6．执行下面的框图，输出的结果s的值为（　　）

A－3

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

填空题 · 4 分

16．一个三棱锥的三视图如图所示，其正视图、侧视图、俯视图的面积分别为4，6，12，则这个几何体的体积为________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

单选题 · 5 分

7．已知向量，．若，则实数m的值为（　　）

A－3

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

继续学习学习下一知识点

下一知识点 : 直线和圆的方程

百度题库 > 高考 > 文科数学 > 立体几何与空间向量

扫码查看完整答案与解析