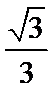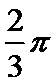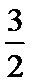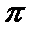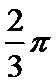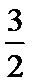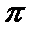- 立体几何与空间向量
- 共2637题
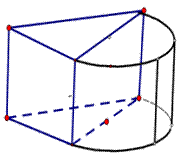
如图,长方体




21.在图中画出这个正方形(不必说明画法与理由);
22.求平面
正确答案

解析
试题分析:分别在

交线围成的正方形
考查方向
解题思路
立体几何解答题在高考中难度低于解析几何,属于得分题,往年第一问多为线面位置关系的证明,今年试题有所创新,改为作截面图.
易错点
截面位置的确定
正确答案

解析
试题分析:长方体被平面


作









考查方向
解题思路
立体几何解答题在高考中难度低于解析几何,属于得分题,往年第一问多为线面位置关系的证明,今年试题有所创新,改为作截面图,令人耳目一新.第二问求两几何体体积之比,方法容易想到,注意运算不要出现错误.
易错点
注意运算正确性
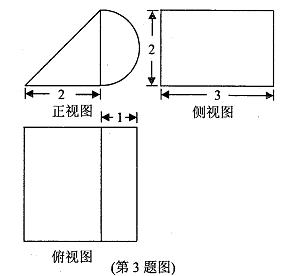
12.已知某三菱锥的三视图如图所示,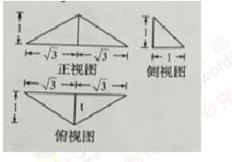
正确答案
解析
由三视图可知该几何体是一个三棱锥,且底面积为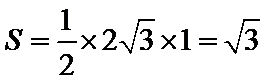
考查方向
解题思路
本题考查三视图,考查几何体体积,考查学生的识图能力.解题时要求我们根据三视图想象出几何体的形状,由三视图得出几何体的尺寸,为此我们必须掌握基本几何体(柱、锥、台、球)的三视图以及各种组合体的三视图.
易错点
本题易在观察三视图的量的时候出错。
知识点
7.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )
正确答案
解析
四棱锥的直观图如图所示:
由三视图可知,



考查方向
解题思路
几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,结合直观图求相关几何量的数据,可得答案.
易错点
几何体框空间结构的判断
知识点
5.一个几何体的三视图如图所示,则该几何体的表面积为( )
正确答案
解析
由几何体的三视图可知该几何体为圆柱的截去一半,所以该几何体的表面积为

考查方向
解题思路
解题时要看清楚是求表面积还是求体积,否则很容易出现错误.本题先根据三视图判断几何体的结构特征,再计算出几何体各个面的面积即可.
易错点
所给几何体空间结构的判断
知识点
3.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于( )cm3
正确答案
解析
将三视图画出直方图然后在旋转为立体图形。为三棱柱和半个圆柱。体积为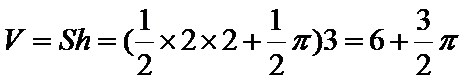
考查方向
解题思路
将三视图画出直方图然后在旋转为立体图形。
易错点
看成三棱锥,而出现错误。
知识点
11.如图(3)所示,侧棱与底面垂直,且底面为正方形的四棱柱ABCD-A1B1C1D1中,AA1=2,AB=1,M、N分别在AD1、BC上移动,始终保持MN∥平面DCC1D1,设BN=x,MN=y,则函数y=f(x)的图像大致是
正确答案
解析
由题意可知,函数的解析式是
考查方向
解题思路
作出辅助线,找到两者之间的关系,从而找到函数满足的图像。
易错点
y与x之间的函数关系式不会求。
知识点
7.如图
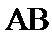
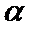
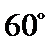
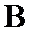
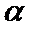
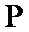
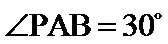
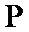
正确答案
解析
试题分析:用垂直于圆锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面和圆锥的一条母线平行时,得到抛物线.
此题中平面α上的动点P满足∠PAB=30°,可理解为P在以AB为轴的圆锥的侧面上,
再由斜线段AB与平面α所成的角为60°,可知P的轨迹符合圆锥曲线中椭圆定义.
故可知动点P的轨迹是椭圆。故选C.
考查方向
解题思路
根据题意,∠PAB=30°为定值,可得点P的轨迹为一以AB为轴线的圆锥侧面与平面α的交线,则答案可求.
易错点
正确理解空间角的关系.
知识点
15.已知直三棱柱



柱
正确答案
解析
设侧面
柱


考查方向
解题思路
根据题意先作出示意图,再来计算最小值。
易错点
不会转化。
知识点
10. 甲几何体(上)



正确答案
解析
由三视图可知:该几何体是由上下两部分组成的,上面是一个球,下面是一个圆锥

考查方向
由三视图求面积、体积
解题思路
由三视图可知:该几何体是由上下两部分组成的,上面是一个球,下面是一个圆锥.利用体积计算公式即可得出.
易错点
空间几何立体感不强
知识点
11.某四棱柱的三视图如图所示,则该四棱柱的体积为___________.
正确答案
解析
由题意得
考查方向
解题思路
由已知三视图分析底面积与高 ,进而利用体积公式计算
易错点
分清底面积
知识点
在空间,下列命题正确的是
正确答案
解析
由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
知识点
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
(1)利用所给数据求年需求量与年份之间的回归直线方程
(2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量。
温馨提示:答题前请仔细阅读卷首所给的计算公式及说明.
正确答案
(1)
解析
(1)由所给数据看出,年需求量与年份之间是近似直线上升,下面来配回归直线方程,为此对数据预处理如下:
对预处理后的数据,容易算得
由上述计算结果,知所求回归直线方程为
即
(2)利用直线方程①,可预测2012年的粮食需求量为

知识点
三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正视图(如图3所示)的面积为8,则该三棱柱外接球的表面积为
正确答案
解析
略
知识点
已知正方形








正确答案
-1,-2
解析
略
知识点
已知菱形




正确答案
解析
略
知识点
扫码查看完整答案与解析