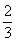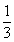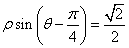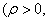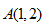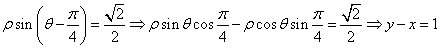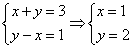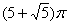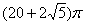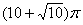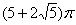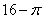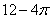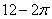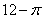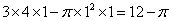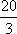- 立体几何与空间向量
- 共2637题
如图，底面是等腰梯形的四棱锥E—ABCD中，EA
（1）设F为EA的中点，证明：DF//平面EBC；
（2）若AE=AB=2，求三棱锥—CDE的体积。
正确答案
见解析。
解析
知识点
一个长方体被一平面截去一部分所得几何体的三视图如右图，
则该几何体的体积是：
正确答案
解析
略
知识点
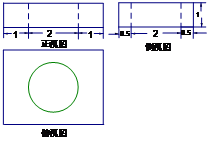
若一个空间几何体的三视图如图所示，则这个几何体的表面积为（）
A
B4
C
D8
正确答案
解析
略
知识点
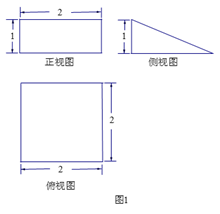
某空间几何体的三视图及尺寸如图1，则该几何体的体积是
A2
B1
C
D
正确答案
解析
略
知识点
若以直角坐标系的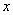
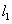
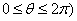
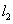
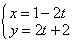
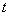
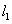
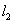
正确答案
解析
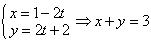
知识点
一个几何体的三视图如图1，则该几何体
的体积为
A
B
C
D
正确答案
解析
略
知识点
如图
（1）求证：
（2）求证：
（3）求五面体
正确答案
见解析。
解析
（1）证明：连接
∵
∴
∵
∴
∵
∴
∴四边形
∴
∵
∴
（2）证法1：取
由（1）知，
∴四边形
∴
在Rt△
∴
在△
∴
∴
∴
∵四边形
∴
∵
∴
证法2：在Rt△
∴
在△
∴
∴
∵
∴
∵
∴
∵
∴
∵四边形
∴
∵
∴
（3）
解：连接
在Rt△
∴
由（2）知
∴
∵
∴
∴四棱锥
∴三棱锥
∴五面体
知识点
如图,正方形ADEF所在平面和等腰梯形所在平面ABCD垂直,已知BC=2AD=4,
（1）
（2）求异面直线BE与AF所成的角;
（3）求该几何体的表面积。
正确答案
见解析。
解析
知识点
某几何体的三视图如右图所示，则该几何体的表面积为
A
B
C
D
正确答案
解析
略
知识点
某几何体的三视图如图所示，则它的体积为______.
正确答案
16
解析
略
知识点
某个长方体被一个平面所截，得到的几何体的三视图如图所示，则这个几何体的体积为（）
A4
B
C
D8
正确答案
解析
略
知识点
一简单组合体的三视图如图（2）所示，则该组合体的
体积为
A
B
C
D
正确答案
解析
由三视图知，此组合体为一个长为4，宽为3，高为1的长方体、中心去除一个半径为1的圆柱，故其体积为
知识点
平面直角坐标系中，方程
正确答案
解析
略
知识点
如图是一个几何体的三视图，若它的体积是3
A
B
C
D
正确答案
解析
由三视图可知此几何体为一个三棱柱，其直观图如图：底面三角形ABC为底边AB边长为2的三角形，AB边上的高为AM=a，侧棱AD⊥底面ABC，AD=3，
∴三棱柱ABC﹣DEF的体积V=S△ABC×AD=
∴a=
故选C。
知识点
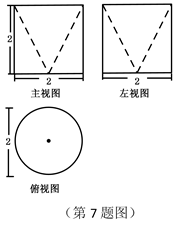
某几何体的主视图与俯视图如图所示，左视图与主视图相同，且图中的四边形都是边长为2的正方形，两条虚线互相垂直，则该几何体的体积是
A
B
C
D
正确答案
解析
略
知识点
扫码查看完整答案与解析