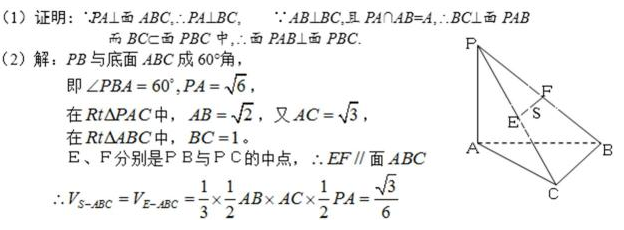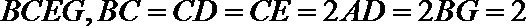立体几何与空间向量_章节学习

1

题型：单选题

|

单选题 · 5 分

3．一个几何体的三视图如图所示，则该几何体的体积为（）

A2

B1

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：简答题

|

简答题 · 12 分

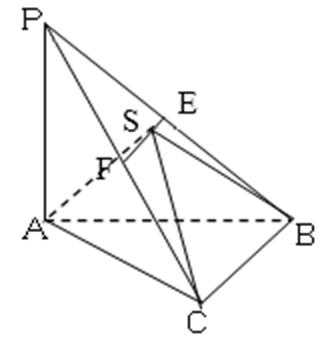
17．三棱锥P−ABC中，PA⊥平面ABC，AB⊥BC。

（1）证明：平面PAB⊥平面PBC；

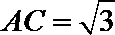
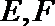
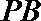
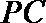
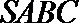
（2）若，，PB与底面ABC成60°角，分别是与的中点，是线段上任意一动点（可与端点重合），求多面体的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题直线与平面垂直的判定与性质平面与平面垂直的判定与性质线面角和二面角的求法

1

题型：简答题

|

简答题 · 12 分

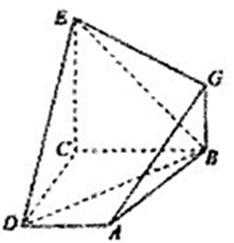
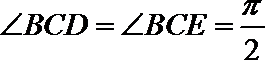
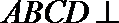
17．如图，已知四边形ABCD和BCEG均为直角梯形，AD//BC,CE//BG，且，平面平面

求证：（I）；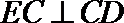

（II）求证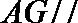：平面BDE；

（III）求：几何体EG-ABCD的体积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题直线与平面平行的判定与性质直线与直线垂直的判定与性质平面与平面垂直的判定与性质

1

题型：单选题

|

单选题 · 5 分

4．已知某几何体的侧视图与其正视图相同，相关的尺寸如下图所示，则这个几何体的体积是（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：简答题

|

简答题 · 13 分

20．在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，且AC=AD=CD=DE=2，AB=1

（1）请在线段CE上找到点F的位置，使得恰有直线BF∥平面ACD，并证明这一事实；

（2）求多面体ABCDE的体积；

（3）求直线EC与平面ABED所成角的正弦值。

正确答案

（1）

如图，由已知AB⊥平面ACD，DE⊥平面ACD，

∴AB//ED，

设F为线段CE的中点，H是线段CD的中点，

连接FH，则，∴，

∴四边形ABFH是平行四边形，

∴，

由平面ACD内，平面ACD，

平面ACD

（2）取AD中点G，连接CG．

AB平面ACD，

∴CGAB

又CGAD

∴CG平面ABED，即CG为四棱锥的高， CG=

∴=2=．

（3）连接EG，由（2）有CG平面ABED，

∴即为直线CE与平面ABED所成的角，

设为，则在中，

有．

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题直线与平面平行的判定与性质直线与平面垂直的判定与性质线面角和二面角的求法

1

题型：填空题

|

填空题 · 4 分

14．一个空间几何体的三视图(单位：)如图所示，则该几何体的体积为______．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：简答题

|

简答题 · 12 分

18．如图，正方形边长为2，平面，，，为的中点.

（Ⅰ）若，求几何体的体积;

（Ⅱ）求证：平面.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题直线与平面平行的判定与性质直线与平面垂直的判定与性质

1

题型：单选题

|

单选题 · 5 分

4．给出如图所示的程序框图，那么输出的数是（）

A7203

B7500

C7800

D7406

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题

1

题型：单选题

|

单选题 · 5 分

7.已知几何体其三视图（如图），若图中圆半径为1，等腰三角形腰为3，则该几何体表面积为（）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：单选题

|

单选题 · 5 分

7．如下图，某简单几何体的正（主）视图与侧（左）视图都是边长为1的正方形，且其体积为，则该几何体的俯视图可以是（）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：单选题

|

单选题 · 5 分

4．一几何体的三视图如图所示，其体积为（　　）cm3．

A12

B36

C18

D20

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：单选题

|

单选题 · 5 分

3.一个几何体按比例绘制的三视图如图所示（单位：m）,该几何体的体积为（　）．

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：单选题

|

单选题 · 5 分

6．一个几何体的正视图、侧视图、俯视图如图所示，则该几何体的表面积和体积分别为（）

A

B和

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：单选题

|

单选题 · 5 分

2.一个几何体的三视图如图所示，则该几何体的体积为（）

A36+12π

B36+36π

C36+48π

D36+6π

正确答案

A

解析

该几何体是一个组合体，其中上面的几何体是一个圆锥,底面半径是3,高是4,下面的几何体是一个棱柱,其中底面是边长为3的正方形，高为4，故该几何体的体积V=3×3×4+×π×32×4=36+12π.

知识点

组合几何体的面积、体积问题简单空间图形的三视图

1

题型：填空题

|

填空题 · 5 分

12. 已知某几何体的三视图如图所示，若该几何体的体积为24,则正视图中的值为______

正确答案

6

解析

解析已在路上飞奔，马上就到！

知识点

组合几何体的面积、体积问题简单空间图形的三视图

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点