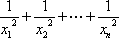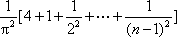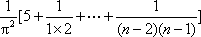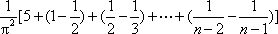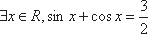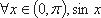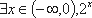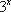- 立体几何与空间向量
- 共2637题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数f(x)=x2e-x.
(1)求f(x)的极小值和极大值;
(2)当曲线y=f(x)的切线l的斜率为负数时,求l在x轴上截距的取值范围。
正确答案
(1) 极小值为f(0)=0,极大值为f(2)=4e-2; (2) (-∞,0)∪[
解析
(1)f(x)的定义域为(-∞,+∞),
f′(x)=-e-xx(x-2),①
当x∈(-∞,0)或x∈(2,+∞)时,f′(x)<0;
当x∈(0,2)时,f′(x)>0.
所以f(x)在(-∞,0),(2,+∞)单调递减,在(0,2)单调递增。
故当x=0时,f(x)取得极小值,极小值为f(0)=0;
当x=2时,f(x)取得极大值,极大值为f(2)=4e-2.
(2)设切点为(t,f(t)),
则l的方程为y=f′(t)(x-t)+f(t)。
所以l在x轴上的截距为m(t)=
由已知和①得t∈(-∞,0)∪(2,+∞)。
令h(x)=

当x∈(-∞,-2)时,h(x)的取值范围是(-∞,-3)。
所以当t∈(-∞,0)∪(2,+∞)时,m(t)的取值范围是(-∞,0)∪[
综上,l在x轴上的截距的取值范围是(-∞,0)∪[
知识点
如图,三棱锥A﹣BCD中,AB⊥平面BCD,CD⊥BD。
(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A﹣MBC的体积。
正确答案
见解析。
解析
(1)证明:∵AB⊥平面BCD,CD⊂平面BCD,
∴AB⊥CD,
∵CD⊥BD,AB∩BD=B,
∴CD⊥平面ABD;
(2)解:∵AB⊥平面BCD,BD⊂平面BCD,
∴AB⊥BD。
∵AB=BD=1,
∴S△ABD=
∵M为AD中点,
∴S△ABM=

∵CD⊥平面ABD,
∴VA﹣MBC=VC﹣ABM=

知识点
如图,三棱柱
(1)证明:平面
(2)平面
正确答案
见解析
解析
(1)由题设知BC⊥






由题设知



又∵




∴面

(2)设棱锥





由三棱柱

∴

知识点
已知函数f(x)=xcos x-sin x+1(x>0)。
(1)求f(x)的单调区间;
(2)记xi为f(x)的从小到大的第i(i∈N*)个零点,证明:对一切n∈N*,有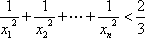
正确答案
见解析。
解析
(1)f′(x)=cos x-xsin x-cos x=-xsin x.
令f′(x)=0,得x=kπ(k∈N*)。
当x∈(2kπ,(2k+1)π)(k∈N)时,sin x>0,此时f′(x)<0;
当x∈((2k+1)π,(2k+2)π)(k∈N)时,sin x<0,此时f′(x)>0.
故f(x)的单调递减区间为(2kπ,(2k+1)π)(k∈N),单调递增区间为((2k+1)π,(2k+2)π)(k∈N)。
(2)由(1)知,f(x)在区间(0,π)上单调递减。
又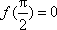
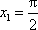
当n∈N*时,因为f(nπ)f((n+1)π)=[(-1)nnπ+1][(-1)n+1(n+1)π+1]<0,
且函数f(x)的图象是连续不断的,所以f(x)在区间(nπ,(n+1)π)内至少存在一个零点,又f(x)在区间(nπ,(n+1)π)上是单调的,故nπ<xn+1<(n+1)π。
因此,
当n=1时,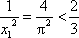
当n=2时,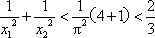
当n≥3时,
<
<
<
=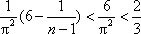
综上所述,对一切n∈N*,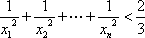
在第(1)问中,通过已知条件,借助导数,转化为判断导数在(0,+∞)上的符号,进而得出函数的单调区间;在第(2)问中,充分利用第(1)问的结论,得到f(x)在(nπ,(n+1)π)上存在零点,从而得出nπ<xn+1<(n+1)π,然后分n=1,n=2,n≥3三;种情况讨论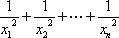

知识点
已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是( )
正确答案
解析
由三视图得,该三棱锥底面面积S=


知识点
在平面直角坐标系xOy中,若曲线




正确答案
解析
根据






知识点
平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为,则此球的体积为( )
正确答案
解析
略
知识点
函数

正确答案
解析
略
知识点
已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
正确答案
解析
略
知识点
下列命题中的真命题是 ( )
正确答案
解析
略。
知识点
如果函数





正确答案
解析
求


知识点
如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为
个几何体的体积为 ( )
正确答案
解析
由三视图还原几何体可知
知识点
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点,且
(1)求证:CN∥平面AMB1;
(2)求证:B1M⊥平面AMG。
正确答案
见解析。
解析
(1)设AB1 的中点为P,连结NP、MP
∵CM


∴CNPM是平行四边形,∴CN∥MP
∵CN

(2)∵CC1⊥平面ABC,∴平面CC1 B1 B⊥平面ABC,
∵AG⊥BC,∴AG⊥平面CC1 B1 B,∴B1M⊥AG
设:AC=2a,则
同理,
∵ BB1∥CC1,∴BB1⊥平面ABC,∴BB1⊥AB,
知识点
扫码查看完整答案与解析