- 立体几何与空间向量
- 共2637题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
一个几何体的三视图如图所示(单位:
正确答案
4
解析
知识点
一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________ m3。
正确答案
30
解析
由几何体的三视图可知:该几何体的顶部为平放的直四棱柱,底部为长、宽、高分别为4 m,3 m,2 m的长方体。
∴几何体的体积V=V棱柱+V长方体=
知识点
若定义在R上的偶函数



正确答案
解析
因为函数





知识点
执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )
正确答案
解析
当t∈[-2,0)时,执行以下程序:t=2t2+1∈(1,9],S=t-3∈(-2,6];当t∈[0,2]时,执行S=t-3∈[-3,-1],因此S∈(-2,6]∪[-3,-1]=[-3,6],故选D.
知识点
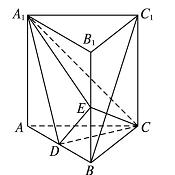
在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形。
(1)若AC⊥BC,证明:直线BC⊥平面ACC1A1;
(2)设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论。
正确答案
见解析
解析
(1)因为四边形ABB1A1和ACC1A1都是矩形,
所以AA1⊥AB,AA1⊥AC.
因为AB,AC为平面ABC内两条相交直线,
所以AA1⊥平面ABC.
因为直线BC⊂平面ABC,所以AA1⊥BC.
又由已知,AC⊥BC,AA1,AC为平面ACC1A1内两条相交直线,
所以BC⊥平面ACC1A1.
(2)取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点。
由已知,O为AC1的中点。
连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线。
所以,MD

因此MD
连接OM,从而四边形MDEO为平行四边形,
则DE∥MO.
因为直线DE⊄平面A1MC,MO⊂平面A1MC,
所以直线DE∥平面A1MC.
即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC.
知识点
设变量x,y满足约束条件
正确答案
解析
由约束条件可得可行域:
对于目标函数z=3x-2y,
可化为
要使z取最小值,可知过A点时取得。
由

∴z=3×0-2×2=-4。
知识点
若0<x1<x2<1,则( )
正确答案
解析
设f(x)=ex-ln x,则
当x=1时,x·ex-1>0,因此在(0,1)上必然存在x1≠x2,使得f(x1)=f(x2),因此A,B不正确;设



知识点
如图,在直三棱柱ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点。
(1)求异面直线CC1和AB的距离;
(2)若AB1⊥A1C,求二面角A1-CD-B1的平面角的余弦值。
正确答案
(1) 
解析
(1)
如图所示,因AC=BC,D为AB的中点,故CD⊥AB。
又直三棱柱中,CC1⊥面ABC,故CC1⊥CD,所以异面直线CC1和AB的距离为
(2)解法一:由CD⊥AB,CD⊥BB1,故CD⊥面A1ABB1,从而CD⊥DA1,CD⊥DB1,故∠A1DB1为所求的二面角A1-CD-B1的平面角。
因A1D是A1C在面A1ABB1上的射影,又已知AB1⊥A1C,由三垂线定理的逆定理得AB1⊥A1D,从而∠A1AB1,∠A1DA都与∠B1AB互余,因此∠A1AB1=∠A1DA,所以Rt△A1AD∽Rt△B1A1A。因此

从而

所以在△A1DB1中,由余弦定理得

(2)解法二:
如图,过D作DD1∥AA1交A1B1于D1,在直三棱柱中,由(1)知DB,DC,DD1两两垂直,以D为原点,射线DB,DC,DD1分别为x轴、y轴、z轴的正半轴建立空间直角坐标系D-xyz.
设直三棱柱的高为h,则A(-2,0,0),A1(-2,0,h),B1(2,0,h),C(0,



由




故





设平面A1CD的法向量为m=(x1,y1,z1),则m⊥

取z1=1,得m=(
设平面B1CD的法向量为n=(x2,y2,z2),则n⊥

取z2=-1,得n=(
所以cos〈m,n〉=
所以二面角A1-CD-B1的平面角的余弦值为
知识点
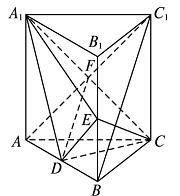
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点。
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=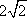
正确答案
见解析
解析
(1)连结AC1交A1C于点F,则F为AC1中点。
又D是AB中点,连结DF,则BC1∥DF.
因为DF⊂平面A1CD,BC1
所以BC1∥平面A1CD.
(2)
因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD.
由已知AC=CB,D为AB的中点,所以CD⊥AB.
又AA1∩AB=A,于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,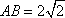
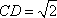
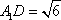
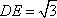
故A1D2+DE2=A1E2,即DE⊥A1D.
所以VC-A1DE=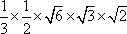
知识点
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为棱DD1上的一点。
(1)求三棱锥A-MCC1的体积;
(2)当A1M+MC取得最小值时,求证:B1M⊥平面MAC。
正确答案
见解析
解析
(1)由长方体ABCDA1B1C1D1知,
AD⊥平面CDD1C1,
故点A到平面CDD1C1的距离等于AD=1。
又∵
∴
(2)
将侧面CDD1C1绕DD1逆时针转90°展开,与侧面ADD1A1共面(如图),
当A1,M,C′共线时,A1M+MC取得最小值。
由AD=CD=1,AA1=2,得M为DD1中点。
连结C1M,在△C1MC中,

∴CC12=MC12+MC2,得∠CMC1=90°,即CM⊥MC1。
又由长方体ABCD-A1B1C1D1知,B1C1⊥平面CDD1C1,
∴B1C1⊥CM。
又B1C1∩C1M=C1,∴CM⊥平面B1C1M,得CM⊥B1M。
同理可证,B1M⊥AM,
又AM∩MC=M,∴B1M⊥平面MAC。
知识点
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=
正确答案
略
解析
(1)证明:
因为

所以
因为
又
所以
(2)由(1)可知
在
又因为
所以四边形ABCE为矩形,
所以
又
所以
知识点
若曲线
正确答案
2
解析



知识点
椭圆C:


(1)求椭圆C的方程;
(2)如图,A,B,D是椭圆C的顶点,P是椭圆C上除顶点外的任意点,直线DP交x轴于点N直线AD交BP于点M,设BP的斜率为k,MN的斜率为m,证明2m-k为定值。
正确答案
见解析
解析



将①代入
又直线AD的方程为
①与②联立解得
由
所以MN的分斜率为m=

知识点
扫码查看完整答案与解析