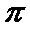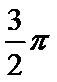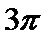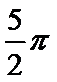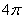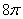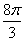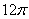立体几何与空间向量_章节学习

1

题型：填空题

|

填空题 · 5 分

某四棱柱的三视图如图所示，则该四棱柱的体积为___________.

正确答案

3/2

知识点

棱柱的结构特征

1

题型：单选题

|

单选题 · 5 分

4. 体积为8的正方体的顶点都在同一球面上，则该球面的表面积为( )

A

B

C

D

正确答案

A

解析

因为正方体的体积为8，所以棱长为2，所以正方体的体对角线长为，所以正方体的外接球的半径为，所以球面的表面积为，故选A.

考查方向

正方体的外接球，球的表面积.

解题思路

棱长为的正方体的外接球，正方体得体对角线是外接球直径，即2R=

易错点

球的表面积公式。

知识点

棱柱的结构特征

1

题型：单选题

|

单选题 · 5 分

11．在正三棱柱ABC-A1B1C1中，若AB=2，AA1=1，则点A到平面A1BC的距离为（）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

棱柱的结构特征

1

题型：单选题

|

单选题 · 5 分

6．在长方体中，．若分别为线段，的中点，则直线与平面所成角的正弦值为（）

A

B

C

D

正确答案

C

解析

如图，过作联结，则即为所求的角

为直角三角形，设则，，所以

，

知识点

棱柱的结构特征线面角和二面角的求法

1

题型：填空题

|

填空题 · 5 分

12．在一个密封的容积为1的透明正方体容器内装有部分液体，如果任意转动该正方体，液面的形状都不可能是三角形，那么液体体积的取值范围是________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱的结构特征棱柱、棱锥、棱台的体积

1

题型：填空题

|

填空题 · 5 分

13．某长方体的对角线长是4，有一条棱长为1，那么该长方体的最大体积为________________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

棱柱的结构特征棱柱、棱锥、棱台的体积

1

题型：填空题

|

填空题 · 4 分

已知一个圆锥的侧面展开图是一个半径为，圆心角为的扇形，则此圆锥的体积为

正确答案

解析

略

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：单选题

|

单选题 · 5 分

某几何体的三视图如图所示，它的体积为(　　)

A72π

B48π

C30π

D24π

正确答案

C

解析

由三视图知该几何体是由一个半球和一个圆锥构成的组合体，∴其体积V＝×33＋×32×4＝30π。

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：单选题

|

单选题 · 5 分

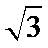
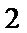
12. 正方体ABCD—A1B1C1D1的棱长为，在正方体表面上与点A距离是的点形成一

条封闭的曲线，这条曲线的长度是

A

B

C

D

正确答案

D

解析

正方体的各个面根据与球心位置关系分为两类：ABCD、AA1DD1、AA1BB1为过球心的截面，截痕为大圆弧，各弧圆心角为60度，所以根据弧长公式可以求得

考查方向

正方体的结构特征

解题思路

找到正方体的外接圆的圆心和半径，实际上是求球在正方体各个面上交线的长度计算。

易错点

空间想象能力和计算能力

知识点

棱柱的结构特征定义法求轨迹方程

1

题型：简答题

|

简答题 · 12 分

已知矩形是圆柱体的轴截面，分别是下底面圆和上底面圆的圆心，母线长与底面圆的直径长之比为，且该圆柱体的体积为，如图所示。

（1）求圆柱体的侧面积的值；

（2）若是半圆弧的中点，点在半径上，且，异面直线与所成的角为，求的值。

正确答案

（1）（2）

解析

（1）设圆柱的底面圆的半径为，依据题意，有，

∴　，

∴。

（2）设是线段的中点，联结，则，

因此，就是异面直线与所成的角，即，

又，，

∴，

∴

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：简答题

|

简答题 · 13 分

如图5，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，是AC的中点，已知，.

（1）求证：OD//平面VBC；

（2）求证：AC⊥平面VOD；

（3）求棱锥的体积.

正确答案

见解析。

解析

（1）∵ O、D分别是AB和AC的中点，∴OD//BC .

又面VBC，面VBC，∴OD//平面VBC.

（2）∵VA=VB，O为AB中点，∴.

连接，在和中，,

∴≌VOC ，∴=VOC=90， ∴.

∵, 平面ABC, 平面ABC, ∴VO⊥平面ABC.

∵平面ABC，∴.

又∵，是的中点，∴.

∵VO平面VOD，VD平面VOD，，∴ AC平面DOV.

（3）由（2）知是棱锥的高，且.

又∵点C是弧的中点，∴，且，

∴三角形的面积，

∴棱锥的体积为，

故棱锥的体积为.

知识点

旋转体（圆柱、圆锥、圆台）棱柱、棱锥、棱台的体积直线与平面平行的判定与性质直线与平面垂直的判定与性质

1

题型：填空题

|

填空题 · 4 分

若一个圆锥的侧面展开图是面积为的半圆面，则该圆锥的体积为________.

正确答案

解析

略

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：填空题

|

填空题 · 4 分

已知圆锥的底面半径为，体积是，则圆锥的侧面积等于

正确答案

解析

略

知识点

旋转体（圆柱、圆锥、圆台）

1

题型：单选题

|

单选题 · 5 分

若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为、,则∶=…………………………………………………………( )

A1∶1

B2∶1

C3∶2

D4∶1

正确答案

C

解析

(探究性理解水平/圆柱的表面积，球的表面积)设球的半径为，圆柱表面积，球表面积,所以.

知识点

旋转体（圆柱、圆锥、圆台）球的体积和表面积

1

题型：单选题

|

单选题 · 5 分

已知圆锥的正视图和侧视图都是边长为4的等边三角形，则此圆锥的表面积是

A

B

C

D

正确答案

D

解析

略

知识点

旋转体（圆柱、圆锥、圆台）简单空间图形的三视图

热门试卷

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点