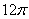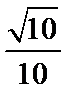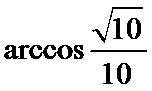- 立体几何与空间向量
- 共2637题
如图5，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，
（1）求证：OD//平面VBC；
（2）求证：AC⊥平面VOD；
（3）求棱锥
正确答案
见解析。
解析
（1）∵ O、D分别是AB和AC的中点，∴OD//BC .
又
（2）∵VA=VB，O为AB中点，∴
连接
∴
∵
∵
又∵
∵VO平面VOD，VD平面VOD，
（3）由（2）知
又∵点C是弧的中点，∴
∴三角形
∴棱锥
故棱锥
知识点
若一个圆锥的侧面展开图是面积为
正确答案
解析
略
知识点
一个圆锥的底面积为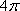
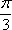
正确答案
解析
略
知识点
一个几何体的三视图如图所示，其中主视图和左视图都是边长为2的正三角形，
俯视图为圆，那么该几何体的表面积为（ ）
A6
B4
C3
D2
正确答案
解析
略
知识点
已知圆锥的正视图和侧视图都是边长为4的等边三角形，则此圆锥的表面积是
A
B
C
D
正确答案
解析
略
知识点
平面直角坐标系中，方程
正确答案
解析
略
知识点
若圆锥的侧面积为
正确答案
解析
略
知识点
8．侧面展开图是半径长为
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知圆锥的底面半径
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
20．如图，圆锥的顶点是
（1）计算圆锥的侧面积；
（2）求
正确答案
（1）
所以，
（2）
解析
解析已在路上飞奔，马上就到！
知识点
8．一个几何体的三视图及尺寸如图所示，其中正视图、侧视图都是等腰三角形，俯视图是圆，则该几何体的表面积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．如果圆锥的侧面展开图是半圆，那么这个圆锥的顶角（圆锥轴截面中两条母线的夹角）是（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11. 如图，有一圆柱开口容器（下表面封闭），其轴截面
A 
B
C 
D
正确答案
解析
如图，展开后作辅助线，使得QC=CP,则AQ即为所求最小距离，利用勾股定理可得D选项是正确的。
考查方向
解题思路
将图像展开之后，通过等价转化，最后变成两点间的距离来求解。
易错点
1、不知道怎样将圆柱展开。
知识点
19．如图，圆锥的顶点为
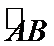
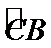
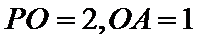
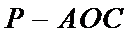
正确答案
三棱锥
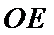
解析
解：
所以∠PAC为异面直线PA与OE所成的角或其补角.
由PO=2,OA=OC=1,得PA=PC=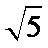
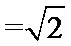
在△PAC中，由余弦定理得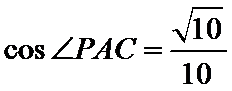
故异面直线PA与OE所成角的大小为
知识点
11. 如图，有一圆柱开口容器（下表面封闭），其轴截面
A 
B
C 
D
正确答案
解析
如图，展开后作辅助线，使得QC=CP,则AQ即为所求最小距离，利用勾股定理可得D选项是正确的。
考查方向
解题思路
将图像展开之后，通过等价转化，最后变成两点间的距离来求解。
易错点
1、不知道怎样将圆柱展开。
知识点
扫码查看完整答案与解析