- 等比数列的判断与证明
- 共100题
16.对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知数列






(1)求

(2)设


正确答案
见解析
解析
解: (1)令

化简得:

由题意得
整理得:


(2)由(1)知,


知识点
21.已知数列{



(Ⅰ)求数列{

(Ⅱ)设


(Ⅲ)在(Ⅱ)的条件下,设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数



(1)求函数
(2)若数列



(3)在(2)的条件下,证明:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设等差数列



(1)证明:数列
(2)若







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.给出数表
正确答案
2,6,18,54
解析
解析已在路上飞奔,马上就到!
知识点
22.已知抛物线





(1)求证:


(2)设


正确答案
解:(1)设直线的方程为:
联立方程可得

设





而

即


(2)由


即得:

由(1)中②代入得

解析
解析已在路上飞奔,马上就到!
知识点
19.设数列


(1)设

(2)求数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在不等边△ABC中,设A.B.C所对的边分别为a,b,c,已知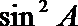
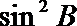
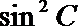
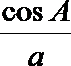
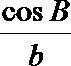
(1)试根据下列选项作出判断,并在括号内填上你认为是正确选项的代号( )
A.是等比数列而不是等差数列
B.是等差数列而不是等比数列
C.既是等比数列也是等差数列
D.既非等比数列也非等差数列
(2)证明你的判断
正确答案
(1)B
(2)因为

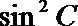
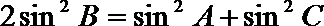
所以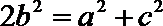
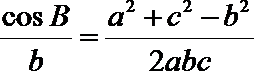

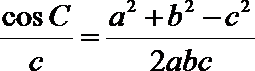
显然
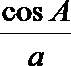
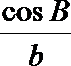
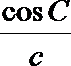
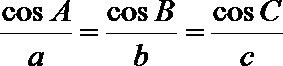

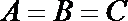
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析