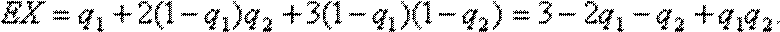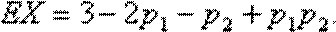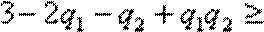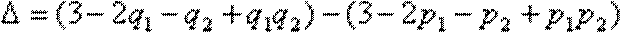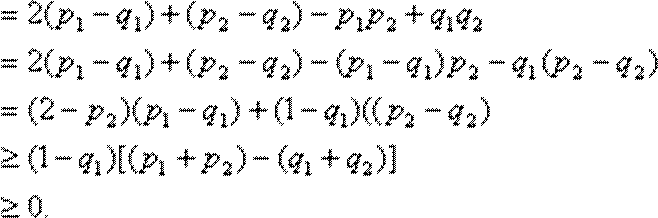- 分式不等式的解法
- 共83题
若变量x、y满足约束条件:
正确答案
15
解析
作出可行域如右图阴影部分,直线2x+y=15与x+3y=27的交点为
M(3.6,7.8),当直线z=x+y+3经过点M时,z=14.4。由于x、y∈N*,∴z∈N*,∴z的最小值为15,此时x=3,y=9.
知识点
已知变量


正确答案
解析
如图,点






知识点
设变量x,y满足

正确答案
解析
画出可行域,根据图形可知当x=5,y=15时2x+3y最大,最大值为55,故选D
知识点
某分公司经销某种品牌产品,每件产品的成本为



(1)求分公司一年的利润

(2)当每件产品的售价为多少元时,分公司一年的利润


正确答案
(1)
解析
解析:(1)分公司一年的利润L(万元)与售价x的函数关系式为:

(2)
令


①当




②当

…………11分
∴ 当



知识点
7.设x,y满足约束条件


正确答案
解析
略。
知识点
某公司为了实现2015年1000万元利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额




正确答案
见解析
解析
由题意,符合公司要求的模型只需满足:当x∈[10,1000]时
①函数为增函数;②函数的最大值不超过5;③y≤x•25%
(1)y=0.025x,易知满足①,但当x>200时,y>5不满足公司要求;…2分
(2)y=1.003x,易知满足①,但当x>600时,y>6不满足公司要求;…4分
(3)
当x∈[10,1000]时,
对于③,设


所以,只有
知识点
设不等式


(1)求

(2)求函数

正确答案
见解析。
解析
(1)不等式

所以,不等式


(2)函数的定义域为


当且仅当

知识点
17.工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别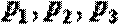
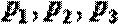
(1)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为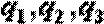
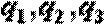
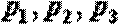
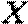
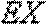
(3)假定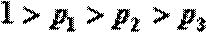
正确答案
见解析。
解析
(1)无论以怎样的顺序派出人员,任务不能被完成的概率都是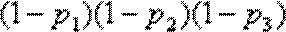
(2)当依次派出的三个人各自完成任务的概率分别为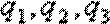

所需派出的人员数目的均值(数学期望)EX是
(3)(方法一)由(II)的结论知,当以甲最先、乙次之、丙最后的顺序派人时,
根据常理,优先派出完成任务概率大的人,可减少所需派出的人员数目的均值.
下面证明:对于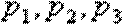
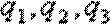
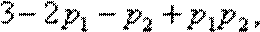
事实上,
即(*)成立.
(方法二)(i)可将(2)中所求的EX改写为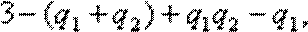
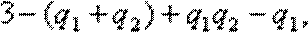
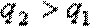
(ii)也可将(2)中所求的EX改写为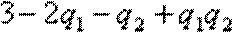
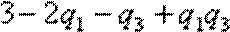
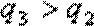
序综合(i)(ii)可知,当
知识点
7.设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知集合


(1)求
(2)若

正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析