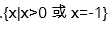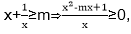- 分式不等式的解法
- 共83题
1.设集合


正确答案
(-1,2)
解析
解析已在路上飞奔,马上就到!
知识点
15. 已知集合A=

(1) 当

(2) 当



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知常数m满足-2≤m≤2,则不等式x+
正确答案
解析
由Δ=m2-4≤0,
(1)若Δ=0,则m=±2,不等式
即为
(2)若Δ<0,则x2-mx+1>0,
由
综合(1)(2)得,不等式的解集为{x|x>0或x=-1}.
知识点
15.已知常数m满足-2≤m≤2,则不等式x+ ≥m的解集为 .
正确答案
解析
由Δ=m2-4≤0,
(1)若Δ=0,则m=±2,不等式
即为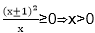
(2)若Δ<0,则x2-mx+1>0,
由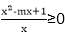
综合(1)(2)得,不等式的解集为{x|x>0或x=-1}.
知识点
12.关于



正确答案
(1,2)
解析
解析已在路上飞奔,马上就到!
知识点
9.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数




正确答案
解析
由



所以函数

而不等式

所以

考查方向
解题思路
1、先通过题中

2、将题中不等式


易错点
1、不会通过

2、忽视题中函数
知识点
2.已知全集U=R,集合

正确答案
解析
∵




考查方向
本题主要考查了集合的补集运算以及分式不等式的解法,考查学生基础知识的掌握能力,在近几年的各省高考题出现的频率较高,常与一元二次不等式、分式不等式、绝对值不等式、指数不等式、对数不等式的求解等知识点交汇命题.属于容易题,也属于易错题.
解题思路
先化简集合




易错点
1.分式不等式转化为整式不等式求解时要考虑分母不为零的情况;
2.求一个集合的补集时,要注意“

知识点
不等式
正确答案
解析
设



知识点
若







正确答案

解析
略
知识点
扫码查看完整答案与解析