简单曲线的极坐标方程
共53题

· 简单曲线的极坐标方程

简单曲线的极坐标方程
共53题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

参数方程为参数和极坐标方程所表示的图形分别是（）

A圆和直线

B直线和直线

C椭圆和直线

D椭圆和圆

正确答案

解析

略

知识点

简单曲线的极坐标方程

题型：填空题

填空题 · 5 分

已知曲线C1：和曲线C2：，则C1上到C2的距离等于的点的个数为　　。

正确答案

解析

将方程与化为直角坐标方程得与x﹣y﹣2=0，

可知C1为圆心在坐标原点，半径为r=的圆，C2为直线，因圆心到直线x﹣y﹣2=0的距离为=，

故满足条件的点的个数n=3，

故答案为 3。

知识点

简单曲线的极坐标方程

题型：单选题

单选题 · 5 分

在平面直角坐标系中，点的直角坐标为.若以原点为极点，x轴正半轴为极轴建立极坐标系，则点的极坐标可以是（）

正确答案

解析

略

知识点

简单曲线的极坐标方程

题型：填空题

填空题 · 5 分

在极坐标系中，直线过点（1，0）且与直线（ρ∈R）垂直，则直线的极坐标方程为　　。

正确答案

解析

解：由题意可知直线（ρ∈R）的直角坐标方程为：x﹣y=0，

过点（1，0）且与直线x﹣y=0垂直的直线方程为：y=﹣（x﹣1），

即所求直线普通方程为x+y﹣1=0，

则其极坐标方程为。

故答案为：。

知识点

简单曲线的极坐标方程

题型：填空题

填空题 · 5 分

已知点是曲线上任意一点，则点到直线的距离的最小值是________.

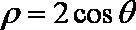
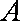
正确答案

解析

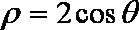
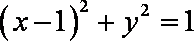
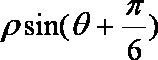
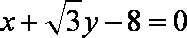
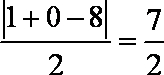
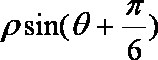
曲线即，直线=4，即，圆心（1，0）到直线的距离等于，所以点A到直线=4的距离的最小值是

知识点

简单曲线的极坐标方程

题型：简答题

简答题 · 10 分

以直角坐标系的原点为极点O，轴正半轴为极轴，已知点P的直角坐标为(1,5),点C的极坐标为,若直线L经过点P,且倾斜角为，圆C的半径为4.

（1）求直线l的参数方程及圆C的极坐标方程；

（2）试判断直线l与圆C有位置关系.

正确答案

见解析。

解析

（1）直线的参数方程，即（为参数）

由题知点的直角坐标为，圆半径为，

∴圆方程为将代入

得圆极坐标方程 ………5分

（2）由题意得，直线的普通方程为，

圆心到的距离为，

∴直线与圆相离。 ………10分

知识点

直线与圆的位置关系简单曲线的极坐标方程点的极坐标和直角坐标的互化直线的参数方程

题型：简答题

简答题 · 12 分

在平面直角坐标系xOy中，已知曲线，以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线.

（1）将曲线上的所有点的横坐标、纵坐标分别伸长为原来的、2倍后得到曲线试写出直线的直角坐标方程和曲线的参数方程；

（2）在曲线上求一点，使点到直线的距离最大，并求出此最大值。

正确答案

（1）

（2）

解析

（1）由题意知，直线的直角坐标方程为：2x-y-6=0，………………2分

∵曲线的直角坐标方程为：，

∴曲线的参数方程为：.………………5分

（2）设点P的坐标，则点P到直线的距离为：

………………7分

∴当sin(600－θ)=-1时，点P(-，此时.…………10分

知识点

函数的图象与图象变化点到直线的距离公式简单曲线的极坐标方程点的极坐标和直角坐标的互化

题型：简答题

简答题 · 10 分

在平面直角坐标系xOy中，已知曲线C的参数方程是（α是参数），若以O为极点，x轴的正半轴为极轴，取与直角坐标系中相同的单位长度，建立极坐标系，求曲线C的极坐标方程。

正确答案

见解析。

解析

由消去θ，得x2+（y﹣1）2=1，

曲线C是以（0，1）为圆心，半径等于1的圆，

所以在极坐标系下，曲线C是以为圆心，半径等于1的圆。

所以曲线C的极坐标方程是ρ=2sinθ，

知识点

简单曲线的极坐标方程圆的参数方程

题型：简答题

简答题 · 10 分

在直角坐标系中，圆的参数方程为参数），以为极点，轴的非负半轴为极轴建立极坐标系。

（1）求圆的极坐标方程；

（2）直线的极坐标方程是，射线与圆的交点为，与直线的交点为，求线段的长。

正确答案

见解析

解析

（1）圆的普通方程为，又

所以圆的极坐标方程为

（2）设，则有解得

设，则有解得

所以

知识点

直线与圆相交的性质简单曲线的极坐标方程参数方程化成普通方程圆的参数方程

题型：简答题

简答题 · 10 分

在直角坐标系中，已知点，直线的参数方程是

（为参数），以为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方

程是。

（1）将圆的极坐标方程化为直角坐标方程，并写出圆心的极坐标

（2）若直线与圆交于两点，求的值。

正确答案

见解析

解析

解：（1）∵，

∴ ，∴，

∴圆的直角坐标方程为：，

圆心的直角坐标为，极坐标为；

（2）直线的参数方程可写为：（为参数），

代入圆的直角坐标方程中得：，

设两点所对应的参数分别为，则，

∴。

知识点

直线与圆相交的性质简单曲线的极坐标方程点的极坐标和直角坐标的互化直线的参数方程

继续学习学习下一知识点

下一知识点 : 平面直角坐标轴中的伸缩变换

百度题库 > 高考 > 理科数学 > 简单曲线的极坐标方程

扫码查看完整答案与解析