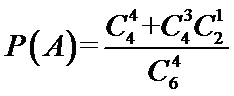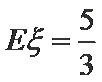- 随机事件的频率与概率
- 共73题
17. 一个袋中装有7个大小相同的球,其中红球有4个,编号分别为1,2,3,4;蓝球3个,编号为2,4,6,现从袋中任取3个球(假设取到任一球的可能性相同).
(

(II)记

正确答案
见解析
解析
考查方向
解题思路
本题的解题思路
1)使用排列组合知识写出基本事件空间和含有编号为2的球个数,并用古典概型的概率公式计算概率
2)分清
3)根据情况依次求概率
4)写分布列以及期望
易错点
本题易错在第一问分类不清,第二问把超几何分布当成二项分布
知识点
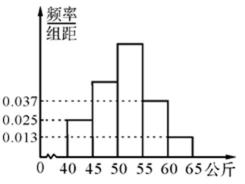
人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
18.求该校抽取的学生总数以及第2组的频率;
19.用这些样本数据估计全市高二学生(学生数众多)的体重.若从全市高二学生中任选5人,设X表示这5人中体重不低于55公斤的人数,求X的分布列和数学期望.
正确答案
(Ⅰ)0.25;
解析
试题分析:本题属于概率的基本问题,题目的难度是逐渐由易到难,(1)按解题步骤求解,(2)要准确判定该变量服从二项分布.
(Ⅰ)设该校抽查的学生总人数为n,第2组、第3组的频率分别为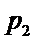
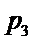
则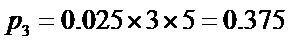

由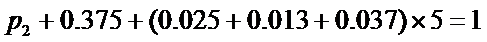
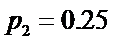
所以该校抽查的学生总人数为240人,从左到右第2组的频率为0.25.
考查方向
解题思路
本题考查离散型随机变量的分布列和期望,解题步骤如下:
1)利用频率分布直方图得到频率和频数;
2)判定该变量服从二项分布;
3)利用二项分布的分布列和期望公式进行求解.
易错点
1)频率直方图中的纵坐标为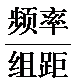
2)不能准确判定该变量服从二项分布.
正确答案
(Ⅱ)分布列略,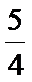
解析
试题分析:本题属于概率的基本问题,题目的难度是逐渐由易到难,(1)按解题步骤求解,(2)要准确判定该变量服从二项分布.
(Ⅱ)由(Ⅰ)知:体重不低于55公斤的学生的概率为
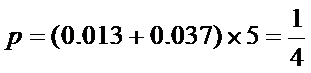
X服从二项分布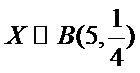
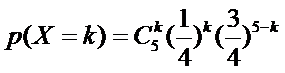
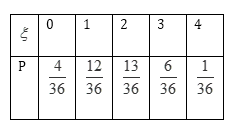
所以随机变量X的分布列为:
则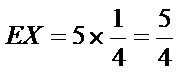
考查方向
解题思路
本题考查离散型随机变量的分布列和期望,解题步骤如下:
1)利用频率分布直方图得到频率和频数;
2)判定该变量服从二项分布;
3)利用二项分布的分布列和期望公式进行求解.
易错点
1)频率直方图中的纵坐标为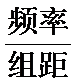
2)不能准确判定该变量服从二项分布.
某企业招聘工作人员,设置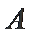

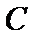
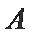
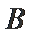

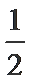
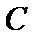
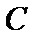
17.求戊竞聘成功的概率;
18.求参加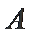
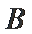
19.记

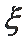
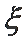
正确答案
解析
设戊竞聘成功为A事件,则 …………1分
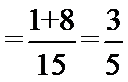
考查方向
解题思路
至少答对3题有两种情况
易错点
事件的性质划分不清,随机变量的取值及相应概率求不准.
正确答案
解析
设“参加
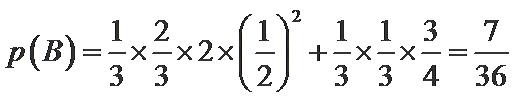
考查方向
解题思路
能出现参加A组测试通过的人数多余参加B组测试通过的人数有两种情况1>0或2>1;
易错点
事件的性质划分不清,随机变量的取值及相应概率求不准.
正确答案
解析
(Ⅲ)
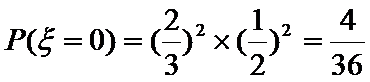
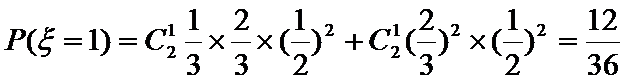


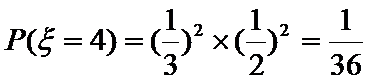
…………12分
∴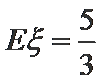
解题思路
根据题意,先确定随机变量可能取值为0,1,2,3,4,然后根据题意,分别求出相应的概率,得到分布列,由分布列求数学期望.
易错点
事件的性质划分不清,随机变量的取值及相应概率求不准.
新生儿Apgar评分,即阿氏评分是对新生儿出生后总体状况的一个评估,主要从呼吸、
心率、反射、肤色、肌张力这几个方面评分,满10分者为正常新生儿,评分7分以下的新
生儿考虑患有轻度窒息,评分在4分以下考虑患有重度窒息,大部分新生儿的评分多在7-10
分之间,某市级医院妇产科对1月份出生的新生儿随机制取了16名,以下表格记录了他们
的评分情况.
19.现从16名新生儿中随机抽取3名,求至多有1名评分不低于9分的概率:
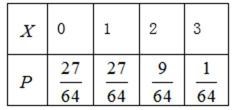
20.以这16名新生儿数据来估计本年度的总体数据,若从本市本年度新生儿中任选3名, 记X表示抽到评分不低于9分的新生儿数,求X的分布列及数学期望.
正确答案
(1)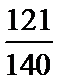
解析
(1)设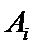
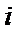
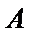
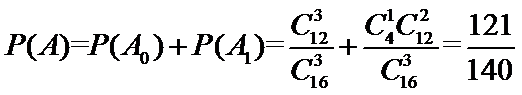
考查方向
解题思路
(1)先表示所求事件再计算其概率(2)写出X的所有可能取值并求出相应概率,列出分布列和计算数学期望。
易错点
所求事件的表示及概率的计算。
正确答案
(2)
解析
(2)由表格数据知,从本本市年度新生儿中任选1名评分不低于9分的概率为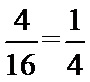
则由题意知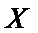
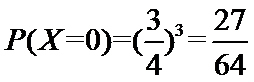
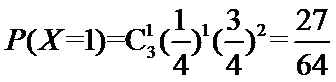

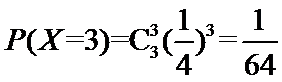
所以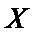
由表格得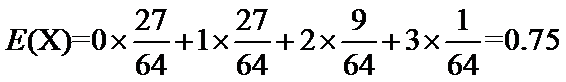
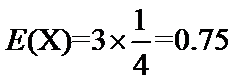
考查方向
解题思路
(1)先表示所求事件再计算其概率(2)写出X的所有可能取值并求出相应概率,列出分布列和计算数学期望。
易错点
所求事件的表示及概率的计算。
经调查发现,人们长期食用含高浓度甲基汞的鱼类会引起汞中毒,其中罗非鱼体内汞含量比其它鱼偏高.现从一批数量很大的罗非鱼中随机地抽出
《中华人民共和国环境保护法》规定食品的汞含量不得超过
18.检查人员从这



19.若从这批数量很大的鱼中任选




正确答案
(1)
考查方向
解题思路
1、第一问属于古典概型,直接用排列组合求出个数;
易错点
容易在排列组合问题计算时出现错误。
正确答案
(2)
解析
(2)依题意可知,这批罗非鱼中汞含量超标的鱼的概率





则


其分布列如下:
所以
考查方向
解题思路
1)第一问属于古典概型,直接用排列组合求出个数;
2)第二问中属于二项分布,各个事件之间是相互独立的,直接用公式求。
易错点
容易在排列组合问题计算时出现错误。
扫码查看完整答案与解析