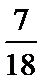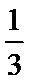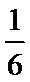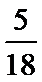- 随机事件的频率与概率
- 共73题
7.2015年高中生技能大赛中三所学校分别有3名、2名、1名学生获奖,
这6名学生要排成一排合影,则同校学生排在一起的概率是 ( )
正确答案
解析
由已知把第一个及第二个学校的学生看做整体得同校学生排在一起共


考查方向
解题思路
1.先求出把第一个及第二个学校的学生看做整体得同校学生排在一起共

易错点
不会相邻问题如何处理;
知识点
2016年上半年,股票投资人袁先生同时投资了甲、乙两只股票,其中甲股票赚钱的概率为



18.求袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率;
19.试求袁先生2016年上半年同时投资甲、乙两只股票的总收益的分布列和数学期望.
正确答案
(1)
解析
(Ⅰ)袁先生2016年上半年同时投资甲、乙两只股票赚钱的概率为
考查方向
解题思路
直接根据题意求即可;
易错点
1.对于题中给出的信息处理出错;2.对于随机变量取值对应的概率出错。
正确答案
((2)
解析
(Ⅱ)用

所以,

考查方向
解题思路
先设出随机变量后写出其取值,然后求其取各个值的概率列分布列带入期望公式即可。
易错点
1.对于题中给出的信息处理出错;2.对于随机变量取值对应的概率出错。
为向国际化大都市目标迈进,沈阳市今年新建三大类重点工程,它们分别是30项基础设施类工程,20项民生

19.求这3人选择的项目所属类别互异的概率;
20.将此3人中选择的项目属于基础设施类工程或产业建设类工程的人数记为


正确答案
解析
记第

由题意知
则
3人选择的项目所属类别互异的概率:
考查方向
解题思路
第一问属于古典概型,直接用排列组合求出个数;
易错点
容易在排列组合问题计算时出现错误。
正确答案
解析
任一名工人选择的项目属于基础设施类或产业建设类工程的概率:
由

其数学期望为
考查方向
解题思路
第二问中属于二项分布,各个事件之间是相互独立的,直接用公式求。
易错点
容易在排列组合问题计算时出现错误。
6. 从3名男同学,2名女同学中任选2人参加体能测试,则选到的2名同学中至少有一名女同学的概率是 .
正确答案
解析
从3名男同学,2名女同学中任选2人参加体能测试的选法有


考查方向
解题思路
1.先利用排列组合求出从3名男同学,2名女同学中任选2人参加体能测试的选法有多少种;
2.利用间接法求出其中选到的2名同学中至少有一名女同学的选法有多少种;3.利用古典概型的概率公式求解。
易错点
1.在求选到的2名同学中至少有一名女同学时只考虑女同学由几个,没有考虑到男同学,导致结果出错;
2.不会间接考虑问题。
知识点
8.若以连续掷两次骰子分别得到的点数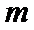
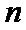
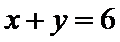
正确答案
解析
以连续掷两次骰子分别得到的点数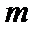
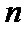

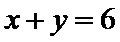
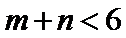
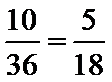
考查方向
解题思路
1.先求出以连续掷两次骰子分别得到的点数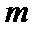
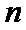
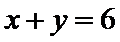
易错点
1.不会计算连续掷两次骰子共有多少种情况;2.不会求点P在直线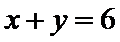
知识点
扫码查看完整答案与解析