- 随机事件的频率与概率
- 共73题
有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复,若上午不测“握力”项目,下午不测“台阶,其余项目上、下午都各测试一人,则不同的安排方式共有种 (用数字作答)。
正确答案
264
解析
本题考查了排列组合及其应用问题,关键是推理与分析的应用,以及分类讨论思维等。
先安排4位同学参加上午的“身高与体重”、“立定跳远”、“肺活量”、“台阶”测试,共有



知识点
将标号为1,2,3,4,5,6的6张卡片放入3个不同的信封中,若每个信封放2张,其中标号为1,2的卡片放入同一信封,则不同的方法共有
正确答案
解析
略
知识点
在样本的频率分布直方图中,一共有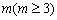

正确答案
解析
略。
知识点
将A,B,C,D,E五种不同的文件放入编号依次为1,2,3,4,5,6,7的七个抽屉内,每个抽屉至多放一种文件,若文件A、B必须放入相邻的抽屉内,文件C、D也必须放在相邻的抽屉内,则所有不同的放法有 ( )
正确答案
解析
略。
知识点
甲、乙、丙三位学生独立地解同一道题,甲做对的概率为

(1)求至少有一位学生做对该题的概率;
(2)求m,n的值;
(3)求
正确答案
(1)
(2)
(3)
解析
解:设“甲做对”为事件



(1)由于事件“至少有一位学生做对该题”与事件“
所以至少有一位学生做对该题的概率是
(2)由题意知

整理得 

由


(3)由题意知



∴


知识点
扫码查看完整答案与解析




