- 利用导数研究函数的单调性
- 共252题
π为圆周率,e=2.71828…为自然对数的底数。
(1)求函数f(x)=
(2)求e3,3e,eπ,πe,3π,π3这6个数中的最大数与最小数。
正确答案
见解析。
解析
(1)函数f(x)的定义域为(0,+∞)。
由f(x)得
当f'(x)>0,即0<x<e时,f(x)单调递增;当f'(x)<0,即x>e时,f(x)单调递减,
所以函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞)。
(2)∵e<3<π,∴eln3<elnπ,πlne<πln3,
从而有ln3e<lnπe,lneπ<ln3π。
于是,根据函数y=lnx,y=ex,y=πx在定义域上单调递增,
可得3e<πe<π3,e3<eπ<3π,
∴这6个数的最大数在π3与3π之中,最小数在3e与e3之中。
由(1)知,f(x)=
∴
得
综上可知,6个数中的最大数是3π,最小数是3e。
知识点
已知


(1)设函数F(x)=18f(x)-x2[h(x)]2,求F(x)的单调区间与极值;
(2)设

(3)设

正确答案
见解析
解析
(1)

令


当



故当






(2)方法一:原方程可化为
即为
①当






此时方程仅有一解
②当




若


若


若

方法二:原方程可化为
即
①当

②当

③当

④当

(3)由已知得

设数列



从而有


又

即对任意



则
知识点
观察








正确答案
解析
由给出的例子可以归纳推理得出:若函数






知识点
若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是( )
正确答案
解析
函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,
∴当x>1时,f′(x)=k﹣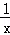
知识点
设函数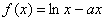
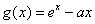
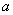
(1)若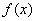
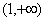
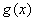

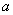
(2)若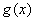

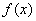
正确答案
见解析
解析
(1)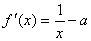
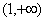
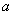
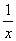
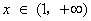
故: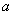
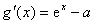
若1≤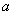
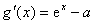
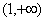
此时,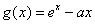

若
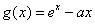
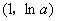
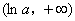
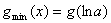
故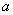

(2)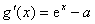

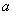
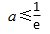
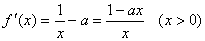
知识点
扫码查看完整答案与解析












