- 利用导数研究函数的单调性
- 共252题
9. 已知




正确答案
解析
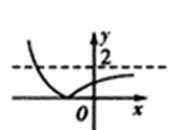
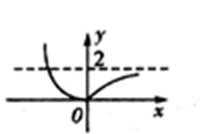
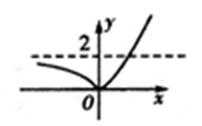
设g(x)=lnx,h(x)=1/x-1,在同一坐标中它们表示的图象如图所示,
要使f(x)=g(x)-h(x)=0,即g(x)=h(x),即它们相交,交点的横坐标就是零点。从图中可以看到,令x=a,时,g(a)>h(a),即f(a)>0,同理可得,f(b)<0,因此此题选C
考查方向
解题思路
此题用图像法解答
易错点
函数零点的概念理解不透彻
知识点
11.若函数
正确答案
解析



考查方向
解题思路
先求出导函数,根据零点存在定理求出在(-1,2)上有极值点时k的范围,再取补集
易错点
区间(-1,2)上没有极值点误解为有极值点
知识点
9. 已知a是常数,函数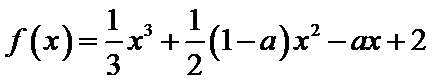
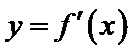
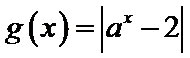
正确答案
解析
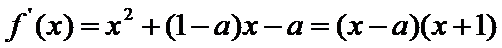

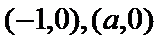

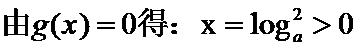
考查方向
本题主要考查了识图/本题主要考查了识图,在高考题中几乎每年都出现,主要考查图像变换:平移变换、对称变换,属于中档题。
解题思路
易错点
1、对应的二次方程不能用十字相乘法分解,并求出两根;
2、搞不清
知识点
19. 已知函数
(Ⅰ)当

(Ⅱ)若关于


正确答案
(Ⅰ)




(Ⅱ)

解析
(Ⅰ)函数


当

令

所以

所以





(Ⅱ)因为关于

令

所以
令

当




而

所以函数
当


所以

当


当



综上,当



法二:
因为关于

所以问题等价于方程
令

令
当


所以函数



所以函数
当


所以函数


当


当

所以函数
综上,当



法三:因为关于

所以问题等价于方程
设函数

令



所以函数


又当


所以函数

所以当


所以
考查方向
本题考查了利用导数求函数的单调性与极值,在近几年的各省高考题出现的频率非常高.
解题思路
(Ⅰ)求出函数

(Ⅱ)将方程解的问题转换为函数存在零点问题.
易错点
未注意到函数的定义域致误.
知识点
21. 设函数

(Ⅰ)当

(Ⅱ)当

正确答案
函数单调减区间为:(Ⅰ)

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”;(3)零点回代是对学生是一种较高的要求.
(Ⅰ)函数

当


得:

所以函数单调增区间为:
,得:
所以函数单调减区间为:
(Ⅱ)若证

即:

设

显然





使得:













∵


∴
考查方向
本题考查了利用导数求函数单调区间的知识,第二问是证明题,过程中要对不等式进行等价变形,本题难在求导后零点不好求,要由零点定理对导数的零点进行分析,将零点关系式回代原函数,求出原函数的正负。
解题思路
1、求导,然后解导数不等式,算极值。
2、对不等式进行等价变形,转化为一个常见函数再进行求导;
3、零点回代。
易错点
1、第二问中卡在求导后解不出零点。2、设出零点后得出零点关系式代入原函数后的正负难以判断。
知识点
扫码查看完整答案与解析