利用导数研究函数的单调性
共252题

· 利用导数研究函数的单调性

利用导数研究函数的单调性
共252题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

12. 已知函数，则函数的大致图像为（）

正确答案

解析

由已知的解析式可知改函数不是奇函数，所以图像不关于原点对称，排除B,C,当x<0时可知函数的导函数恒小于0 ，也就是单调递减的，所以排除D,所以选A答案。

考查方向

函数的图像及性质。

解题思路

根据函数的性质去做。

易错点

不会求解。

知识点

导数的几何意义利用导数研究函数的单调性利用导数求函数的极值

题型：简答题

简答题 · 12 分

21．已知函数，曲线在点处的切线方程为．

（I）求a，b的值；

（II）证明：当x>0，且时，．

正确答案

（1），；（2）见解析。

解析

试题分析：本题属于导数的几何意义及其应用，题目的难度是逐渐由易到难，

（1）根据导数的几何意义，结合已知条件构造方程组即可解出；

（2）利用构造函数之后再求导来证明。

考查方向

本题考查了导数的几何意义及其应用。

解题思路

本题考查导数的性质，解题步骤如下：

（1）根据导数的几何意义，结合已知条件构造方程组即可解出；

（2）利用构造函数之后再求导来证明。

易错点

导函数容易求错。

知识点

利用导数研究函数的单调性利用导数证明不等式

题型：简答题

简答题 · 12 分

21．设函数f（x）＝lnx＋－（a＋1）x，（a∈R）．

（Ⅰ）当a＝时，求函数f（x）的单调区间；

（Ⅱ）当x＞1时，若f（x）＜－x－a （a＞0）恒成立，求实数a的取值范围．

正确答案

（1）的单调递增区间为和，单调递减区间为；

（2）

解析

试题分析：本题属于导数求含参数的函数的单调区间及参数的取值范围的问题，题目的难度是逐渐由易到难，

（1）利用导数与函数的单调性的关系直接求解；

（2）构造函数，再利用导数并分参数a在几类情况下分类来解解：（1）当时，

时，或，时，

的单调递增区间为和，单调递减区间为.

（2）即，

令，，，

当时，，在单调递增，

，而，在大于0恒成立，不满足题意

当时，有零点

当，即时，，在单调递减

，而，在小于0恒成立，满足题意

当，即时，，

在上单调递增，在上单调递减

，令，

在单调递减，

而，在无解，时不成立

综上： …………(12分)

考查方向

本题考查了利用导数求含参数的函数的单调区间及参数的取值范围的问题。

解题思路

本题考查导数求含参数的函数的单调区间及参数的取值范围的问题，解题步骤如下：

（1）利用导数与函数的单调性的关系直接求解；

（2）构造函数，再利用导数并分参数a在几类情况下分类来解。

易错点

第2问不知道怎样转换已知条件。

知识点

利用导数研究函数的单调性利用导数证明不等式

题型：填空题

填空题 · 5 分

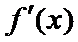
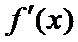
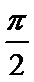
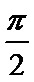
16．已知函数y＝f（x）为R上的偶函数，y＝f（x）的导数为，且当x∈（－∞，0]时，不等式f（x）＋x·＜0成立，若a·f（a）≥sinθ·f（sinθ）对一切θ∈

[－，]恒成立，则实数a的取值范围是__________．

正确答案

解析

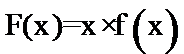
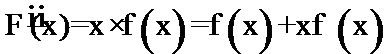
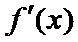
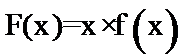
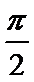
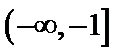
构造函数，则，在当x∈（－∞，0]时，不等式f（x）＋x·＜0成立，而由于函数y＝f（x）为R上的偶函数所以函数是奇函数，对称的区间上函数的单调性相同，所以a·f（a）≥sinθ·f（sinθ）对一切θ∈[－，]恒成立，只要满足a的取值范围。

考查方向

函数的导数与函数的单调性以及求参数的取值范围问题。

解题思路

先构造函数，然后利用所构造的函数将已知要求的参数的取值范围转化为求函数的最值问题。

易错点

不知道构造函数来解答。

知识点

求函数的值利用导数研究函数的单调性利用导数求函数的极值

题型：简答题

简答题 · 12 分

21.已知函数．

(Ⅰ)求函数的最小值；

(Ⅱ)证明: 对一切，都有不等式恒成立．

正确答案

（1）；（2）略；

解析

（Ⅰ）-----------------------------2分

当时，当时，

在在单调递减，在在单调递增，----------------------------------4分

-------------------------------------------------------------5分

（Ⅱ）由（Ⅰ）知----------------------6分

从而--------7分

记

则----------------------------------------9分

当时，当时，

在在单调递增，在在单调递减，--------------------------------10分

故，

故原命题得证. -----------------------------------------------------------------12分

考查方向

本题主要考查利用导数判断函数的单调、求函数的最值等知识，意在考查考生应用导数知识综合解决问题的能力。

解题思路

第（1）问直接根据求函数极值的过程求即可；第（2）问先利用第一问构造函数，然后判断其单调性和最值即可得到要证明的。

易错点

第（2）问无法构造出函数导致无法入手；

第（2）问不知道如何使用第（1）问的结论。

知识点

利用导数研究函数的单调性利用导数求函数的极值利用导数证明不等式

继续学习学习下一知识点

下一知识点 : 利用导数求函数的极值

百度题库 > 高考 > 文科数学 > 利用导数研究函数的单调性

扫码查看完整答案与解析