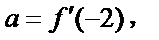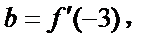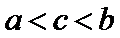- 利用导数研究函数的单调性
- 共252题
21.已知函数




(1)求实数
(2)当



正确答案
(1)
解析
试题分析:本题属于函数与导数的应用,题目的难度是逐渐由易到难,(1)求导之后得到a的一个范围,最后再得到关于a的一个不等式;(2)分类讨论求解。
试题解析:(1)0令
由题意:△

且
∵

∴
(2)又∵
∴


又∵
①当



∴当





∴当

∴
考查方向
解题思路
本题考查了函数与导数的应用,解题步骤如下:(1)求导之后得到a的一个范围,最后再得到关于a的一个不等式;(2)分类讨论求解。
易错点
不会转化为所学的内容来做。
知识点
已知函数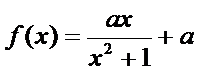

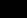
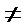
25.求函数f (x)的单调区间;
26.证明:当a > 0时,对于任意x1,x2∈(0,e],总有g(x1) < f (x2)成立,其中
正确答案
(1)当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1);
解析
(Ⅰ)函数f (x)的定义域为R,f ′(x)=
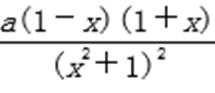
当a>0时,当x变化时,f ′(x),f(x)的变化情况如下表:
当a<0时,当x变化时,f ′(x),f(x)的变化情况如下表:
综上所述,
当a>0时,f (x)的单调递增区间为(-1,1),单调递减区间为(-∞,-1),(1,+∞);
当a<0时,f (x)的单调递增区间为(-∞,-1),(1,+∞),单调递减区间为(-1,1).
考查方向
解题思路
1)第一问对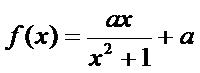
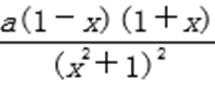
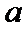
2)第二问由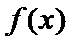
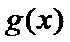
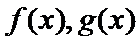
正确答案
(2)略;
解析
(Ⅱ)由(Ⅰ)可知,当a>0时,f (x)在区间(0,1)上单调递增,f (x)
f (x)在区间(1,e]上单调递减,且f (e)=
因为g(x)=aln x-x,所以g′(

①当a≥e时,g′(x)≥0在区间(0,e]上恒成立,
所以函数g(x)在区间(0,e]上单调递增,所以g(x)max=g(e)=a-e<a.
所以对于任意x1,x2∈(0,e],仍有g(x1)<f(x2).
②当0<a
因为a-(aln a-a)=a(2-ln a)>a(2-ln e)=a>0,
所以对任意x1,x2∈(0,e],总有g(x1)<f (x2).
综上所述,对于任意x1,x2∈(0,e],总有g(x1)<f (x2).
考查方向
解题思路
1)第一问对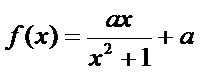
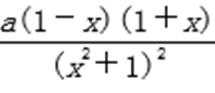

2)第二问由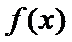
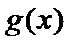
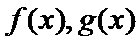
已知函数
24.当

25.当

26.若对于任意的


正确答案
(Ⅰ)当


解析
(Ⅰ)当




当



当



∴当


考查方向
解题思路
直接求导,判断导数的正负后即可得到极值;
易错点
无
正确答案
(Ⅱ)当



当


当



解析
(Ⅱ)当




由



(1)当




(2)当


(3)当



在
综上所述,
当



当


当



考查方向
解题思路
求导后分类讨论导数的正负后确定函数的单调区间;
易错点
在求函数的单调性时,不会确定分类的标准;
正确答案
(Ⅲ)
解析
(Ⅲ)由(Ⅱ)知,当


∴
∵对于任意的

∴

∴

当


∴实数

考查方向
解题思路
先根据第(2)问放缩后构造不等式
易错点
不会放缩
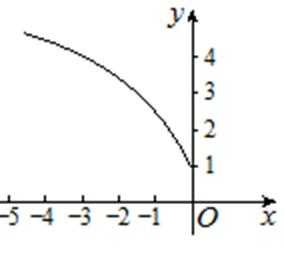
15.函数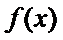
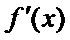
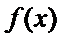
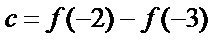
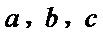
正确答案
解析
由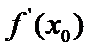
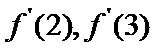
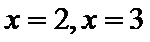
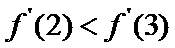
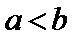
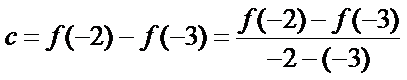
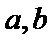
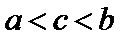
考查方向
解题思路
1)由导函数的几何意义,将导函数转化为切线斜率;
2)由导函数的定义将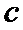
易错点
本题易将导函数图像与原函数图像弄错,容易忘记导函数的定义;
知识点
9.已知函数




正确答案
解析
构造函数








考查方向
解题思路
1.先构造函数

易错点
1.不会利用题中给出的导数的等式构造函数;2.不知道选项中给出的两个数什么关系。
知识点
扫码查看完整答案与解析