等比数列的判断与证明
共122题

· 等比数列的判断与证明

等比数列的判断与证明
共122题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 16 分

22.给定数列，记该数列前项中的最大项为，即；该数列后项中的最小项为，即；．

（1）对于数列：3,4,7,1，求出相应的；

（2）若是数列的前项和，且对任意有其中为实数，且．

①设，证明数列是等比数列；

②若数列对应的满足对任意的正整数恒成立，求实数的取值范围．

正确答案

（1）；

（2）①证明略；②．

解析

（1）当=1时，A1=3，B1=1，从而可求得，

同理可得

（2）①当时，所以

当时，

两式相减得所以

又

所以，数列是以为首项、为公比的等比数列．

②由①知：；

又，

由于

所以由推得

所以对任意的正整数恒成立．

因为所以

由，得，

但且，所以解得，所以

考查方向

本题考查数列的综合应用，突出考查考查推理论证与抽象思维的能力，是难题．数列的综合应用在近几年各省市的高考试卷中频频出现，是高考的热点问题，往往以等差数列、等比数列为载体，涉及递推公式、通项公式、前项和，结合数列单调性、数列恒成立等知识交汇命题．

解题思路

题（1），当=1时，A1=3，B1=1，从而可求得，同理可求得的值；

题（2）①，利用等比数列的定义证明是等比数列，对含有的表达式，先利用（）求得与递推关系，将代入递推关系化简求得，同时验证的初始值，从而证明是等比数列；

题（2）②，由①得到的通项公式，根据求得，从而得到关于不等式，解得的取值范围．

易错点

对含有的表达式，往往利用求通项时容易忽视的要求，同时要验证的初始值；对新定义、的不理解；恒成立问题的恰当转化．

知识点

等比数列的判断与证明数列与不等式的综合

题型：简答题

简答题 · 12 分

18.设数列{an}的前n项和为Sn，己知a1=l，nan+1=(n+2)Sn，n∈N*.求证：是等比数列；设Tn= S1+S2+--+Sn，求证：(n+l) Tn<nSn+1．

正确答案

（1）；

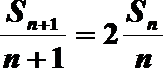
（2）略．

解析

本题属于数列中的基本问题，题目的难度是逐渐由易到难．

（1）由已知得。所以是以1为首项，2为公比的等比数列。

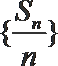
（2）由上知。

……①

……②

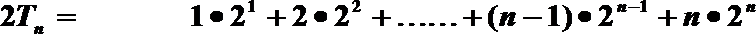
①-②得：。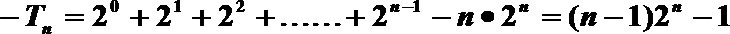

即(n+l) Tn<nSn+1．

考查方向

本题考查了数列的问题．属于高考中的高频考点。

易错点

错位相减法求和时相减的结果项数易错。

知识点

等比数列的判断与证明数列与不等式的综合

题型：单选题

单选题 · 5 分

5．已知数列是等比数列，是1和3的等差中项，则=

正确答案

解析

通过观察，可以看到，b2,b16和b9之间的关系，可以得到=b92, ，又根据等差中项的性质，可以得到b9=(1+3)÷2=2,所以=22=4

考查方向

等比数列的定义及性质，等差中项的性质

解题思路

利用等差中项求b9,进而求解答案

易错点

发现不到b2b16和b9之间的关系。

知识点

等比数列的判断与证明

题型：单选题

单选题 · 5 分

6. 若成等比数列，则下列三个数：① ② ③，必成等比数列的个数为（）

正确答案

解析

由题可知：等比数列的相邻两项相乘仍然是等比数列。

A选项不正确，C选项不正确，D选项不正确，所以选B选项。

考查方向

本题主要考查等比数列的性质

解题思路

代入特值计算或由等比数列的基本性质，即可得到结果。

A选项不正确，C选项不正确，D选项不正确，所以选B选项。

易错点

本题易在代特值时发生错误。

知识点

平面向量数量积的运算等比数列的判断与证明

题型：填空题

填空题 · 5 分

6．设等比数列的前项的和为，若，则的值为_______

正确答案

解析

由等比数列前n项和的性质成等比数列，则成等比数列，，解得．

设等比数列{an}的首项为a1，公比为q．显然q≠1，由题意得

解之得：所以，

考查方向

本题主要考查等比数列的基本运算，等比数列的求和，考查学生的运算能力，难度中等.

解题思路

本题主要考查等比数列的基本运算，等比数列的求和。

解题步骤如下：利用公式或性质，列出等式。正确运算，得出结果。

易错点

本题易错点是公式会弄错，运算上出现错误。

知识点

等比数列的判断与证明

继续学习学习下一知识点

下一知识点 : 等比数列的性质及应用

百度题库 > 高考 > 理科数学 > 等比数列的判断与证明

扫码查看完整答案与解析