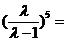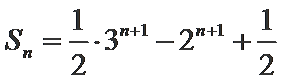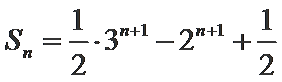- 等比数列的判断与证明
- 共122题
17.已知数列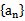
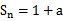
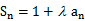
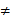
(I)证明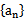
(II)若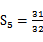
正确答案
见解析
解析
(Ⅰ)由题意得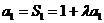
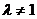
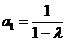
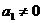
由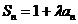
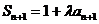
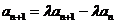
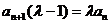
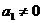
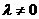
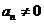
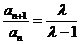
因此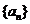
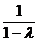
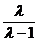
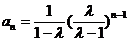
(Ⅱ)由(Ⅰ)得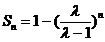
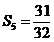
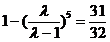
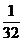
解得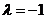
知识点
17.已知无穷等比数列





正确答案
解析



若

若

考查方向
解题思路
先将无穷等比数列前


易错点
对化简之后
知识点
20.设数列A:




(I)对数列A:-2,2,-1,1,3,写出G(A)的所有元素;
(I I)证明:若数列A中存在




(I I I)证明:若数列A满足



正确答案
知识点
11. 已知数列







正确答案
解析
设数列









考查方向
本题主要考查递推数列,数列与函数的关系,等差数列的定义等知识。
知识点
20.设数列{an}满足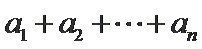
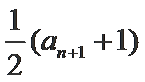
(1)求证数列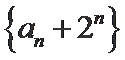
(2)求数列{an}的前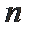
正确答案
(1)略
(2)
解析
(1) 解 由条件可得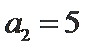
两式相减整理得an+1-3an=2n,则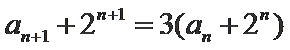
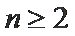
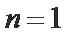
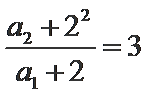
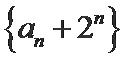
(2)法一:由2Sn=an+1-2n+1+1直接可得
法二:直接求和公式.
考查方向
本题主要考查等比数列的定义以及与之间的关系等知识。
解题思路
利用等式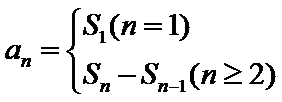
易错点
第一问没有验证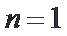
知识点
扫码查看完整答案与解析