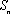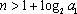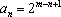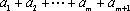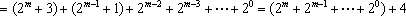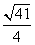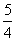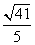- 等比数列的判断与证明
- 共122题
已知数列
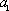
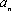
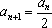
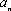
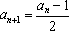
(1)若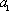
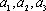
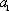
(2)设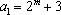
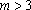
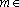
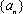
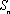
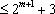
(3)若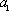
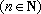
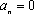
正确答案
见解析
解析
(1)∵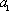

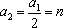
若
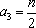
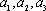
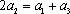
即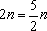
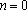

若
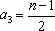
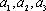
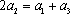
即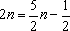
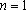
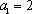
∴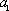
(2)∵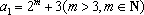
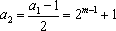
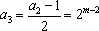
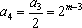
可知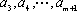
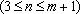
又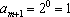
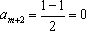
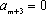
∴当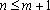
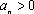
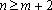
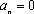
故对于给定的
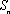
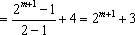
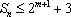
(3)当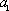
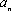
当
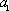
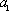
假设当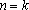
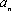
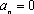
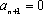
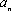
则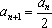
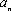
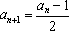
故总有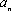
当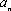
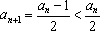
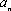
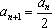
故总有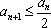
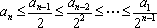
当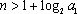
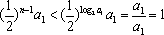
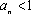
又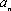
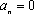
【另法提示:先证“若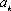

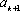
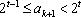
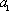

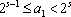
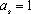
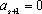
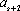
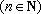
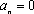
知识点
已知数列







(1)求证:数列
(2)若



(3)当




若





正确答案
见解析
解析
解析:
(1)







(2) 由(1)可得



所以


(3)由(1)当
当


所以对正整数

由




①当

因为

所以存在正整数






相应的


②当



仍为奇数,又

知识点
已知实数m是2,8的等比中项,则双曲线
正确答案
解析
略
知识点
设数列{an}共有n(




(1)当
(2)当
正确答案
见解析。
解析
(1)当

因为



所以


故此时满足条件的数列{an}共有3个:
(2)令bi=(1≤i≤7),则对每个符合条件的数列{an},满足条件:


反之,由符合上述条件的7项数列{bn}可唯一确定一个符合条件的8项数列{an}。
记符合条件的数列{bn}的个数为N。
显然,bi (1≤i≤7)中有k个2;从而有k个
当k给定时,{bn}的取法有
故
因此,符合条件的数列{an}的个数为393。
知识点
数列





(1)证明:

(2)记数列




成立?若存在,求出所有符合条件的有序实数对
正确答案
见解析
解析
(1)方法1:由

两边同时乘以


故

又

方法2:

整理得


(2)由(1)得,

所以
则
因为
当


综上,存在符合条件的所有有序实数对

知识点
两个正数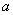
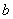
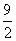
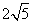
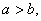
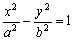
正确答案
解析
略
知识点
某高科技企业研制出一种型号为









(1)求数列


(2)记









正确答案
见解析
解析
(1)由题设,知




故









故


于是,

(2)由(1)知,

当



所以
当

当



所以,当


故该企业需要在第11年年初更换
知识点
已知各项均不为零的数列

正确答案
解析
由

知识点
已知数列



(1)若

(2)若



(3)若



正确答案
见解析
解析
(1)当



所以数列

(2)因为
所以对任意的

所以数列
又因为
所以

所以数列
(3)因为


且对任意的

设



所以数列
记

(其中


当


当
①若



②若



综上,当

当




当


当


当


当


即当

知识点
设首项为1的正项数列




其中
(1)求
(2)求证:数列
(3)证明:“数列




正确答案
见解析
解析
(1)n = 1时,由
若p = 0时,
当



而
(2)当p = 2时,

②


④



所以数列{an}是等比数列,且
(3)充分性:若x =1,y = 2,由






满足
必要性:假设



所以
化简得
显然

因为x、y均为整数,所以当


故当


知识点
扫码查看完整答案与解析