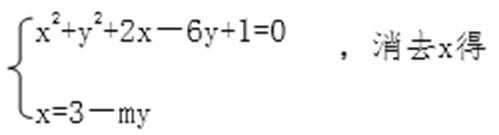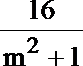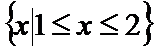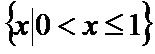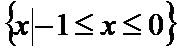- 对数函数的定义域
- 共41题
7.若将函数

正确答案
解析
B
平移后图像表达式为
令

故选B.
考查方向
解题思路
先根据平移变换公式求出平移后的表达式,再根据对称性求出对称轴方程.
易错点
忽略平移变换和伸缩变换都是针对x而言,即x本身加减多少值,而不是依赖于ωx加减多少值导致出错.
知识点
14. 在平面直角坐标系



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)求
(2)求函数的值域;
(3)判断函数的单调区间并证明。
正确答案
(1)
(2)(-1,1)
(3)R上递增
解析
解析已在路上飞奔,马上就到!
知识点
19.已知圆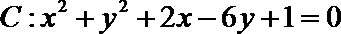
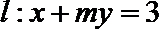
(1)若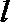
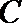
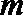
(2)是否存在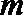
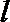
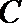
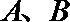
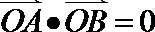
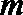
正确答案
(1)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),
半径为 r = 3,
若 l与C相切,
则得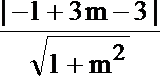
∴(3m-4)2=9(1+m2),
∴m =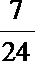
(2)假设存在m满足题意。
由
(m2+1)y2-(8m+6)y+16=0,
由△=(8m+6)2-4(m2+1)·16>0,
得m>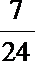
设A(x1,y1),B(x2,y2),
则y1+y2=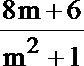
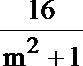
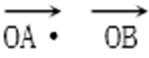
=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·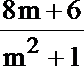
=25-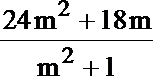
24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2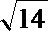
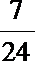
∴存在m=9±2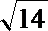
解析
解析已在路上飞奔,马上就到!
知识点
3.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知x轴上有一点列






(I)写出

(II)记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 给出下列四个命题:
①“k =1”是“函数

② 函数


③ 函数
④ 设O是△ABC内部一点,且
其中真命题的序号是( )(写出所有真命题的序号)。
正确答案
④
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合


正确答案
(-1,2)
解析
解析已在路上飞奔,马上就到!
知识点
1.集合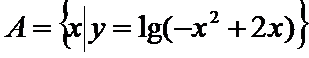

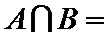
正确答案
解析
由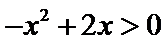

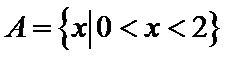


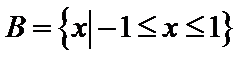
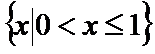
考查方向
解题思路
先分别求出两个集合中代表元素的取值范围,再求交集。
易错点
对集合的代表元素认识不清导致出错。
知识点
扫码查看完整答案与解析