- 对数函数的值域与最值
- 共19题
14.函数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
6.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知双曲线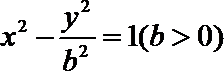

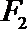
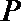
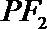
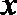
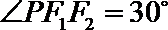
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 等比数列



正确答案
必要非充分
解析
解析已在路上飞奔,马上就到!
知识点
14.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.定义区间





正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
已知函数
(1)当
(2)如果


正确答案
(1)定义域:(-1,3),值域:(-∞,2](2)
解析
(1) 当
令
所以函数

令
所以
因此函数

(2) 解法一:



令
当


当


当





当


当


综上,

解法二:



由


令
所以

因此

知识点
12.设函数

①

②存在





若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
正确答案

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析