- 直线与圆锥曲线的位置关系
- 共144题
4.已知一个空间几何体的三视图如右图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
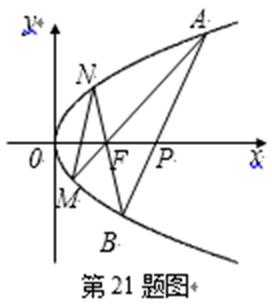
21.如图,已知抛物线






(1)证明
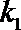


(2)记直线
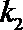

正确答案
证明:(1)依题意,设直线

将其代入

整理得 
从而
于是
∴

又
(2)证明:设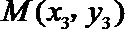
则 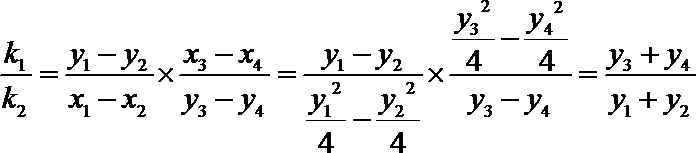
设直线

将其代入

整理得
∴
同理可得 
故
由(1)知,
∴
解析
解析已在路上飞奔,马上就到!
知识点
7.已知点









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知斜率为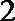
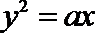
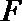
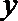
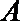
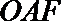
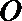
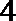
正确答案
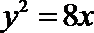
解析
解析已在路上飞奔,马上就到!
知识点
9.直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知点




(Ⅰ)试判断点

(Ⅱ)是否存在过




正确答案
(Ⅰ)因点


所以点




(Ⅱ)解法一:假设存在满足题设的直线



依题意,得
①当直线
②当直线


联立方程组
消去

∴

此时,方程(*)为
∴存在满足题设的直线
且直线


解法二:假设存在满足题设的直线



依题意,得
易判断直线

∴设直线

联立方程组
消去

∵
∴直线与轨迹
又

∴存在满足题设的直线
且直线


解法三:假设存在满足题设的直线



依题意,得
∵

∴有


当


∴


注意到点



∴存在满足题设的直线
且直线


解析
解析已在路上飞奔,马上就到!
知识点
5.过抛物线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析