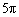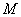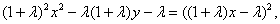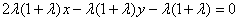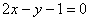- 曲线与方程
- 共215题
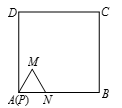
如图放置的边长为
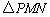
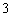
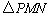
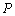
正确答案
解析
略
知识点
如图,已知平面内一动点




(1)求动点

(2)当








①求
②轨迹





正确答案
见解析
解析
(1)当



当
当
(2)以线段


可得轨迹
①解法1:设



要使

当点

解法2:在椭圆




在
配方,得:

得
根据椭圆的对称性,当

当点

②结论:当





下证当






证法1:假设存在这样的两个不同的点
设线段

由于


又
两式相减,得
将该式写为
并将直线


得
①、②得

得
即

此时不存在满足题设条件的点

证法2:假设存在这样的两个不同的点

则

直线

故此时椭圆上不存在两点(除了点


知识点
如图,正方体






正确答案
解析
略
知识点
已知函数

(1)若


(2)求

正确答案
见解析
解析
(1)解:


当


所以曲线


即 
(2)解:方程

(ⅰ)当




上的最小值是

(ⅱ)当





故



………………8分
① 当




上的最小值是

② 当




所以


因为 
所以 当







③ 当



所以



综上,
当




当




当




当




知识点
已知圆





(1)求C的方程;
(2)



正确答案
见解析
解析
由已知得圆





设动圆



(1)∵圆




由椭圆的定义可知,曲线C是以M,N为左右焦点,场半轴长为2,短半轴长为

(2)对于曲线C上任意一点



当且仅当圆P的圆心为(2,0)时,R=2.
∴当圆P的半径最长时,其方程为
当




当












当








当


综上,|AB|=

知识点
已知动圆与直线

(1)求动圆圆心P的轨迹C的方程.
(2)过原点作斜率为1的直线交曲线C于











①令

②数列


正确答案
见解析
解析
知识点
如图,已知⊙





正确答案
2
解析
延长


知识点
设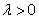
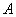

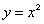
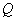
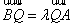
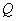
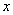
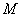
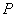
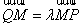
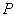
正确答案
P的轨迹方程为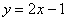
解析
本题考查直线和抛物线的方程,平面向量的概念,性质与运算,动点的轨迹方程等基本知识,考查灵活运用知识探究问题和解决问题的能力,全面考核综合数学素养。
由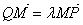
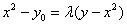

再设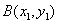

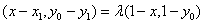

将①式代入②式,消去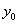
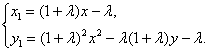
又点B在抛物线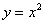
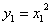
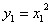
整理得
因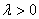
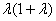
故所求点P的轨迹方程为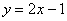
知识点
如图,已知两条抛物线










(1) 证明:
(2)过原点








正确答案
见解析。
解析
本题以二次曲线中的抛物线和直线相关知识为背景,考察学生的运算和推演能力,考查转化化归思想的运用。
(1)设直线l1:y=kx,l2:y=mx(k≠m,k≠0,m≠0)分别代入E1,E2的方程得
A1



一是当k=-m时,直线A1B1与A2B2的斜率都不存在,A1B1‖A2B2;
二是当k

综合可见,A1B1‖A2B2。
(2)设直线l:y=nx,则C1


另一法:由(1)知,两个三角形三边对应平行,它们相似。面积比为边的比的平方。可得。
知识点
已知动圆












(1)求曲线
(2)试探究

(3)记





正确答案
见解析。
解析
(1)设圆心

由于动圆


圆






故圆心


(2)设

由


由




(3)





令








知识点
扫码查看完整答案与解析