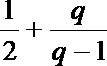- 直线、平面平行的判定与性质
- 共628题
8.在等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.过点A(2,-3),且法向量是
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.一个不透明的袋中装有5个白球、4个红球(9个球除颜色外其余完全相同),经充分混合后,从袋中随机摸出3球,则摸出的3球中至少有一个是白球的概率为( )。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.某产品经过4次革新后,成本由原来的105元下降到60元.如果这种产品每次革新后成本下降的百分率相同,那么每次革新后成本下降的百分率是______(精确到
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,AD

(1)求证:AF∥平面BDE;
(2)求证:平面BDE
正确答案
(1)证明:∵AD⊥平面ABC,AC

∴AD⊥AC,AD⊥AB,
∵AD∥CE,∴CE⊥AC
∴四边形ACED为直角梯形.
又∵∠BAC=90°,∴AB⊥AC,∴AB⊥面ACED.
∴凸多面体ABCED的体积
求得CE=2.
取BE的中点G,连结GF,GD,
则GF∥EC,GF
∴GF∥AD,GF=AD,四边形ADGF为平行四边形,
∴AF∥DG.
又∵GD

∴AF∥平面BDE.
(2)证明:∵AB=AC,F为BC的中点,
∴AF⊥BC.
由(1)知AD⊥平面ABC,AD∥GF,∴GF⊥面ABC.
∵AF
又BC
又∵DG∥AF,∴DG⊥面BCE.
∵DG
解析
解析已在路上飞奔,马上就到!
知识点
10.设复数z=x+yi(x,y
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知
(Ⅰ)求
(Ⅱ)求
正确答案
(1)
(2)原式
解析
解析已在路上飞奔,马上就到!
知识点
7.如图所示的流程图中,输出的结果是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知等差数列{an}公差不为0, 其前n项和为Sn, 等比数列{bn}前n项和为Bn, 公比为q, 且|q|>1, 则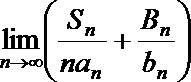
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在
(1)若点P为AB的中点,E为
(2)当棱锥
正确答案
解:
(1)证明:作
由已知得:


所以
(2)设

令
则
由上表易知:当

解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析