- 直线、平面平行的判定与性质
- 共628题
19.如图,在四棱锥





(Ⅰ)求异面直线OC与MD所成角的大小;
(Ⅱ)求点M到平面
正确答案
(Ⅰ)设线段


则

由已知,可得



所以,异面直线OC与MD所成角的大小
(Ⅱ)作





所以,点

解析
解析已在路上飞奔,马上就到!
知识点
14. 如图,已知底面半径为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知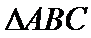
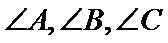
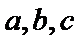
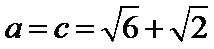
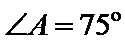
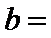
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
20.已知:正方体


(Ⅰ) 求证:
(Ⅱ) 求证:

(Ⅲ)求三棱锥
正确答案
(Ⅰ)证明:连结


∵




又


∵


∴
(Ⅱ)取
∴四边形

∴

(Ⅲ)



解析
解析已在路上飞奔,马上就到!
知识点
5.圆锥的侧面展开图为扇形,若其弧长为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在各项均为正数的等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 在三棱柱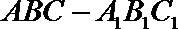

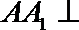
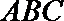
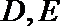
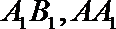
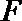


(1)求证: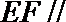

(2)求二面角
正确答案
(1)证明:取

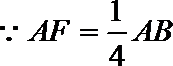
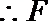
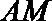
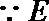
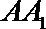

在三棱柱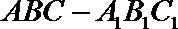



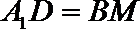
则四边形






则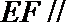
(2)空间直角坐标系,则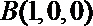

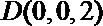
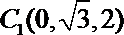
∴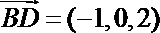
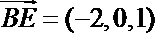

设面BC1D的一个法向量为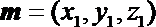
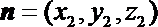
则由


又由

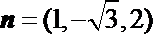
则
故二面角E-BC1-D的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
21. 设集合P=
(1) 试判断

(2) 若

(3) 根据对第(1),(2)小题的研究,请你对属于集合P的函数从函数性质方面提出一个有价值的结论,说明理由;若


正确答案
(1) f1(x)不属于P; f2(x)∈P
(2) b=0
(3) f(x)为奇函数,且f(x)不属于P
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求
(2)若不等式


正确答案
(1)

又

即

(2)






解析
解析已在路上飞奔,马上就到!
知识点
18.设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.
(1)求证:f(x)是周期函数;
(2)当x∈[2,4]时,求f(x)的解析式;
(3)计算f(0)+f(1)+f(2)+…+f(2 011)=0.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析