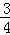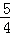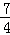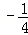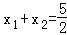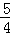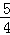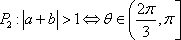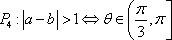- 直线、平面平行的判定与性质
- 共628题
如图,在四棱锥






24.求证:
25.求三棱锥
正确答案
见解析
解析
证明:连接AC,
∵底面ABCD是边长为a的正方形,并且F是BD的中点,
∴F是AC的中点,
在△PAC中,F是AC的中点,E是PC的中点,
∴EF∥PA,
∵平面PAD,平面PAD,
∴EF∥平面PAD.
考查方向
解题思路
利用线面平行的判定定理:连接AC,只需证明EF∥PA,利用中位线定理即可得证;
易错点
线面平行的判定要对线外,线内要进行说明.
正确答案
解析
∵侧面PAD⊥底面ABCD,交线是AD,
在△PAD中,
∴△PAD是等腰直角三角形,
设AD的中点为G,连接PG,则
∴
∴空间几何体BCDP的体积是:
考查方向
解题思路
设AD的中点为G,连接PG,证明PG⊥底面ABCD,可求空间几何体BCDP的体积.
易错点
无
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)-g(x)=x3+x2+1,则f(1)+g(1)=( )。
正确答案
解析
由f(x)与g(x)分别是定义在R上的偶函数和奇函数,知f(-1)=f(1),g(-1)=-g(1)。
又由f(x)-g(x)=x3+x2+1,
令x=-1,得f(-1)-g(-1)=(-1)3+(-1)2+1=1,
即f(1)+g(1)=1.故选C.
知识点
已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为( )
正确答案
解析
∵F是抛物线y2=x的焦点
F(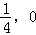
设A(x1,y1) B(x2,y2)
∴|AF|+|BF|=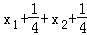
解得
∴线段AB的中点横坐标为
∴线段AB的中点到y轴的距离为
故选C
知识点
在平面直角坐标系xOy中,已知点A(0,-1),B点在直线y = -3上,M点满足

(1)求C的方程;
(2)P为C上的动点,l为C在P点处得切线,求O点到l距离的最小值。
正确答案
(1)曲线C的方程式为y=

(2)o点到
解析
(1)设M(x,y),由已知得B(x,-3),A(0,-1)。
所以


再由题意可知(


所以曲线C的方程式为y=

(2)设P(x







因此直线


则o点到


当

知识点
不等式组的解集记为D,有下面四个命题:
p1:∀(x,y)∈D,x+2y≥-2,
p2:∃(x,y)∈D,x+2y≥2,
p3:∀(x,y)∈D,x+2y≤3,
p4:∃(x,y)∈D,x+2y≤-1.
其中的真命题是( )
正确答案
解析
不等式组表示的区域D如图中的阴影部分所示,设目标函数z=x+2y,根据目标函数的几何意义可知,目标函数在点A(2,-1)处取得最小值,且zmin=2-2=0,即x+2y的取值范围是[0,+∞),故命题p1,p2为真,命题p3,p4为假。
知识点
已知a与b均为单位向量,其夹角为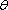
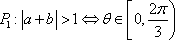
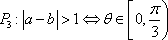
其中的真命题是
正确答案
解析
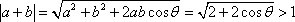
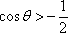
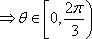

知识点
下列关于开放式基金的说法正确的是( )。
A.规模不固定,但有最低规模要求
B.交易手续费为成交金额的2.5%
C.分红方式有现金分红和再投资分红两种
D.单位资产净值于每个开放日进行公告
E.在期限内不能直接赎回基金,须通过上市交易套现
正确答案
A,C,D
解析
[解析] 选项BE描述的是封闭式基金。
16.如图,在直三棱柱


求证:(1)
(2)
正确答案
证明:(1)由题意知,

又


又因为



所以

(2)因为棱柱
所以

因为


又因为





所以

又因为


因为


因为





又因为


解析
解析已在路上飞奔,马上就到!
知识点
17. 已知






(1)求

正确答案
解析
因为


且

为





所以
所求的几何体是圆锥挖去同轴的一个圆锥剩下的部分。其体积为
考查方向
解题思路
要找PD在面PAC上的射影,PD和其在面PAC上的射影所成的角即为所求。
根据图形易得所得的几何体是圆锥挖去同轴的一个圆锥剩下的部分,再根据三棱锥的体积公式即可求解。
易错点
不容易找到PD在面PAC上的射影。
(2)求△


①弄清楚所求的几何体的形状②体积公式的正确应用。
知识点
扫码查看完整答案与解析