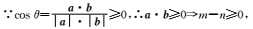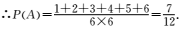- 数量积表示两个向量的夹角
- 共77题
2.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.现有下列命题:
①命题“

②若



③函数

④若非零向量


其中正确命题的序号有__________。
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
8.连掷两次骰子得到的点数分别为m和n,记向量a=(m,n)与向量b=(1,-1)的夹角为θ,则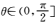
正确答案
解析
知识点
21.已知向量a、b、c是同一平面内的三个向量,其中a=(1,2).
(1)若|c|=2
(2)若|b|=
正确答案
(1)令c=(x,y),则由|c|=2


又由a∥c知,2x-y=0②
联立①②可解得:

故c=(2,4)或c=(-2,-4).
(2)由a+2b与2a-b垂直知(a+2b)·(2a-b)=0,
即2a2+3a·b-2b2=0,∴a·b=
即|a||b|cosθ=

而由a=(1,2)知|a|=

∵θ∈[0,π],∴θ=π.
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知



正确答案
解析
因为向量b与向量c平行,
所以s=(-1)*2=-2.
所以
所以答案为
考查方向
解题思路
先根据向量平行求解出s的值,进而求出余弦值
易错点
向量平行的计算
知识点
14.已知向量a,b满足a·(a-b)=2,且|a|=1,|b|=2,则a与b的夹角等于 .
正确答案
解析
设向量


所以
而|a|=1,|b|=2,所以
所以
又

考查方向
解题思路
1.先将a·(a-b)=2展开表示成
2.将|a|=1,|b|=2带入上式,得到
易错点
1.两个向量夹角的取值范围不清楚导致出错;2.数量积公式不会。
知识点
14.已知向量a=(1,

正确答案
2
解析
根据a=(1,

所以
即
考查方向
解题思路
本题考查平面向量的有关问题,
解题步骤如下:根据向量的坐标表示写出

易错点
1、向量模的求解出错;
2、向量的数量积的定义理解出错。
知识点
12. 已知向量



正确答案
解析
考查方向
解题思路
本题主要是突破点在于垂直与数量积之间的转换
易错点
本题注意向量垂直与数量积之间的转换
知识点
13.向量




正确答案
解析
由



考查方向
本题主要考查向量的相关知识。
解题思路
将垂直条件转化为数量积为0,代入数据求出
易错点
1.不能将垂直的条件进行转化。
2.夹角公式不清楚
知识点
扫码查看完整答案与解析