- 倒序相加法求和
- 共9题
已知函数



(1)求
(2)证明:对任意的

正确答案
见解析。
解析
(1)解:由已知,得
于是
所以
故
(2)证明:由已知,得

即



下面用数学归纳法证明等式

(i)当n=1时,由上可知等式成立。
(ii)假设当n=k时等式成立, 即
因为

所以
所以当n=k+1时,等式也成立。
综合(i),(ii)可知等式

令


所以

知识点
在△ABC中,角A,B,C的对边分别为a,b,c,且2

(1)求cos A的值;
(2)若


正确答案
见解析
解析
(1)由2


即cos(A-B)cos B-sin(A-B)sin B=
则cos(A-B+B)=

(2)由cos A=

由正弦定理,有
所以,sin B=
由题知a>b,则A>B,故
根据余弦定理,有

故向量



知识点
函数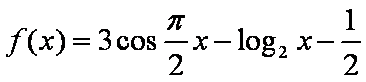
正确答案
解析
在同一坐标系内画出函数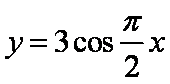
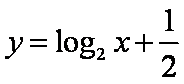
知识点
20.已知A(






(1)求



(2)已知






(3)在(2)的条件下,设









正确答案
解:
(1)∵点M在直线x=

又



∴

① 当






② 当







综合①②得,

(Ⅱ)由(Ⅰ)知,当


∴

n≥2时,




①+②得,2

当n=1时,


(Ⅲ)













∴

当c=1时,
∴1<
∴m=1.
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知数列{an}为等差数列,且满足an+1=an2-nan+1,n=1,2,3,…
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:
(Ⅲ)当





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析























