- 其它方法求和
- 共28题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:
单选题
|
设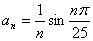
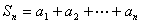
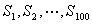
正确答案
C
解析
依据正弦函数的周期性,可以找其中等于零或者小于零的项.
知识点
其它方法求和
1
题型:简答题
|
已知定义在R上的函数



(1)若对任意正整数




(2)设对任意正整数




正确答案
见解析
解析
(1)令

则
令

则
令

即
则
所以,数列


(2)令

则

故

设

所以

从而
则

知识点
抽象函数及其应用其它方法求和
1
题型:简答题
|
设{an}是公比为q的等比数列。
(1)推导{an}的前n项和公式;
(2)设q≠1,证明数列{an+1}不是等比数列。
正确答案
见解析
解析
(1)设{an}的前n项和为Sn,
当q=1时,Sn=a1+a1+…+a1=na1;
当q≠1时,Sn=a1+a1q+a1q2+…+a1qn-1,①
qSn=a1q+a1q2+…+a1qn,②
①-②得,(1-q)Sn=a1-a1qn,
∴
(2)证明:假设{an+1}是等比数列,则对任意的k∈N+,
(ak+1+1)2=(ak+1)(ak+2+1),

a12q2k+2a1qk=a1qk-1·a1qk+1+a1qk-1+a1qk+1,
∵a1≠0,∴2qk=qk-1+qk+1.
∵q≠0,∴q2-2q+1=0,
∴q=1,这与已知矛盾,
∴假设不成立,故{an+1}不是等比数列
知识点
等比数列的判断与证明其它方法求和
下一知识点 : 数列与函数的综合
扫码查看完整答案与解析





