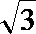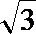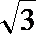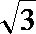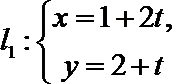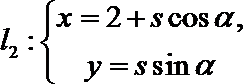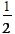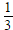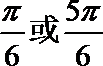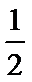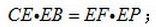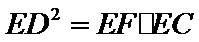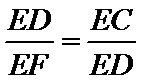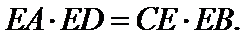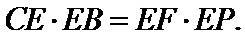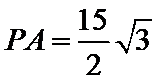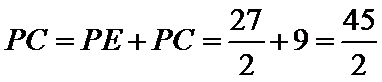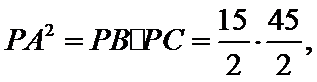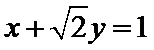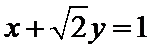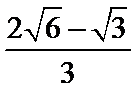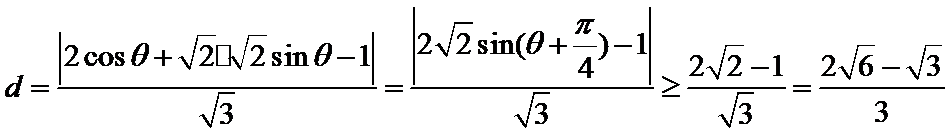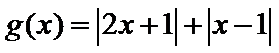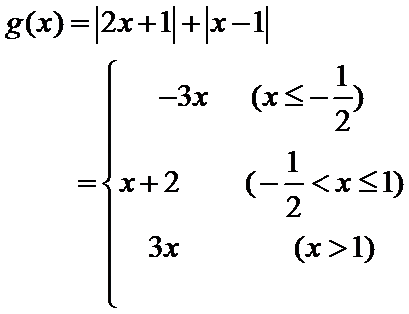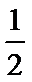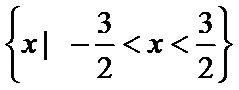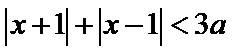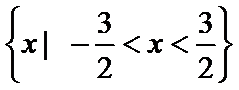- 选修部分
- 共638题
9. 柱坐标(2,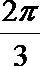
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在
正确答案
解析
Tr+1=



知识点
请考生在第22、23、24三题中任先一题做答,如果多做,则按所做的第一题记分。
22.选修4-4:坐标系与参数方程
已知曲线C的极坐标方程为


23.选修4-5:不等式选讲
已知函数
(1)解不等式f(x)>1
(2)求函数
24.选修4-1:几何证明选讲
如图,在



(1)求证:BE=2AD
(2)求函数AC=1,EC=2时,求AD的长
正确答案
22.
23.略
24.略
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4—1:几何证明选讲
如图,AB是

(1)求证:FG//AC;
(2)若CG=1,CD=4,求
23.选修4-4:极坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为

(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(3,
24.选修4-5:不等式选讲
(1)求不等式
(2)已知
22.选修4—1:几何证明选讲
如图,AB是

(1)求证:FG//AC;
(2)若CG=1,CD=4,求
23.选修4-4:极坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2sin θ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B.若点P的坐标为(3,),求|PA|+|PB|.
24.选修4-5:不等式选讲
(1)求不等式
(2)已知

正确答案
正确答案
正确答案
选做题(14 ~ 15题,只能从中选做一题)
14. (坐标系与参数方程选做题)
直线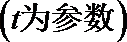
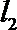
15.(几何证明选讲选做题)
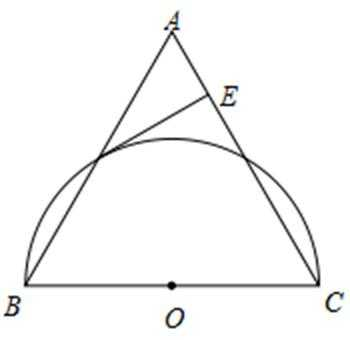
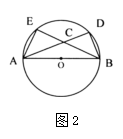
如图,在△ABC中,AB=AC,以BC为直径的半圆O与边AB相交于点D,切线DE⊥AC,
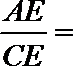
正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14~15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在极坐标系中,直线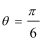
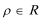
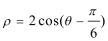
15.(几何证明选讲选做题)
如图(图2)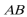
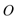
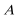
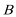
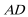
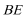
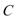
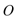
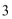
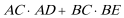
正确答案
14. 2
15. 36
解析
解析已在路上飞奔,马上就到!
知识点
选做题 (14~15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在直角坐标系中,曲线







15.(几何证明选讲选做题)
如图, 








正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
10.计算定积分
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请在第22~24题中任选一题做答。
22.选修4—1:几何证明选讲
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(Ⅰ)求证:△ABE≌△ACD;
(Ⅱ)若AB=6,BC=4,求AE.
23.选修4—4:坐标系与参数方程
已知曲线C的极坐标方程为ρ=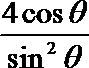
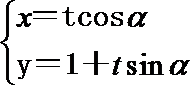
(Ⅰ)把曲线C的极坐标方程和直线l的参数方程化为直角坐标方程,并说明曲线C的形状;
(Ⅱ)若直线l经过点(1,0),求直线l被曲线C截得的线段AB的长.
24.选修4—5:不等式选讲
设函数f(x)=|2x-1|+|ax-3|,x∈R.
(Ⅰ)若a=1时,解不等式f(x)≤5;
(Ⅱ)若a=2时,g(x)=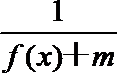
正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
13.二项式(1+sinx)n的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为
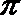
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在极坐标系中,直线


正确答案
2
知识点
从22、23、24题中任选一道作答。
22.选修4-1:几何证明选讲
自圆








试求
23.极坐标与参数方程
已知直线/经过点

(I)写出直线/的参数方程,并把圆C的方程化为直角坐标方程;
(II)设l与圆C相交于两点A、B,求点P到A、B两点的距离之积.
24.不等式选讲
已知

正确答案
22.


又



于是


23.
24.
解析
解析已在路上飞奔,马上就到!
知识点
6. 在平面直角坐标系中,




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.选做题:在A、B、C、D四小题中只能选做2题。解答应写出文字说明、证明过程或演算步骤。
B.(选修4-2:矩阵与变换)
二阶矩阵M有特征值λ=8,其对应的一个特征向量

C.(选修4-4:坐标系与参数方程)
已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,曲线C的极坐标系为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在以下三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
【选修4—1】几何证明选讲(请回答28、29、30题)
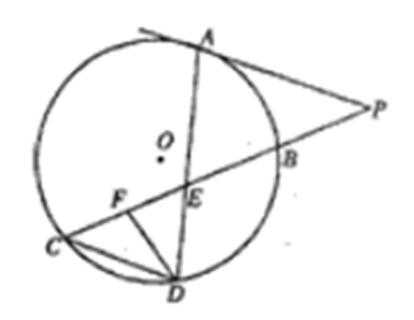
如图:已知PA切圆O于A,PBC是割线,弦CD∥AP,AD交BC于E,F在CE上,且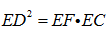
【选修4—4】坐标系与参数方程(请回答31、32题)
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C1的极坐标方程为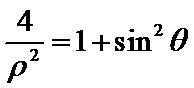
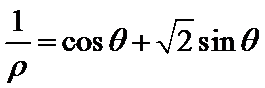
【选修4—5】不等式选讲(请回答33、34题)
已知函数
28.求证:∠EDF=∠P;
29.求证:
30.若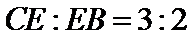
31.写出曲线C1与直线l的直角坐标方程;
32.设Q为曲线C1上一动点,求Q点到直线l距离的最小值。
33.求a的值;
34.解不等式:
正确答案
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
解析
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
考查方向
解题思路
先证明△DEF∽△CED,再根据平行求出∠EDF=∠P.
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴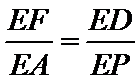
∴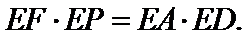
∴
解析
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴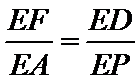
∴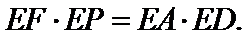
∴
考查方向
解题思路
借助第一问,求得△FED∽△AEP,进而得出成比例线段。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
解析
证明:
设CE=3k,EB=2k.
∵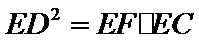
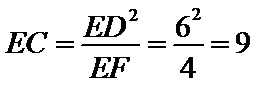
又CE=3k=9, k=3,EB=2k=6.
由(2)得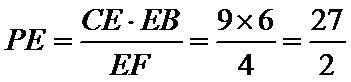
故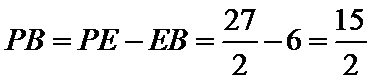
∵
∴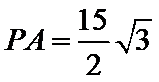
考查方向
解题思路
借助第一二问,根据成比例线段得出结果。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错
正确答案
C1的直角坐标方程: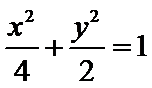
解析
根据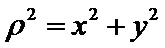
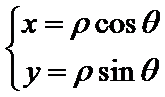
C1的直角坐标方程: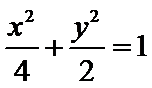
考查方向
解题思路
根据极坐标与直角坐标互化的公式可以直接得到曲线C1与直线l的直角坐标方程;
易错点
极坐标与直角坐标的转化
正确答案
解析
由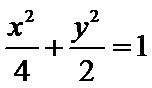
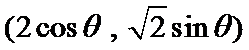
∴点Q到直线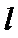
考查方向
解题思路
将曲线C1的直角坐标方程转化为参数方程,代入点Q到直线的距离公式,利用三角恒等变换得到最值。
易错点
点到直线距离公式的应用,计算出错。
正确答案
a=1
解析
可以先不考虑参数a,令
画出图形,即可知道函数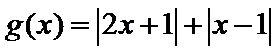
因为函数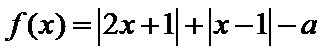
所以a=1
【三级考点】不等式的基本性质,绝对值不等式的解法
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
在对函数的最小值进行求解时,参数的处理容易出错
正确答案
解析
把a=1代入
利用零点分段法可以得到此不等式的解集是
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
解决第二问的时候,要注意不等式的最小值。
扫码查看完整答案与解析