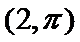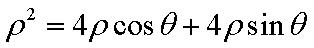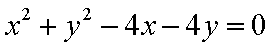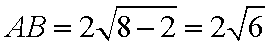- 选修部分
- 共638题
12.在直角坐标系


正确答案
解析
由极坐标方程得


考查方向
解题思路
先将极坐标方程两边同乘以
易错点
极坐标和直角坐标的互化公式记不住出错。
知识点
15.已知直线l的参数方程为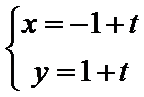
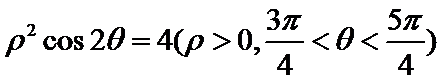
正确答案
解析
直线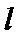
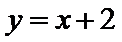
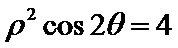
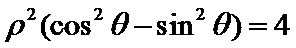
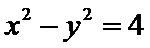
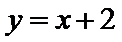
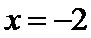
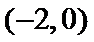
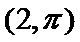
考查方向
解题思路
参数方程主要通过代入法或者已知恒等式(如
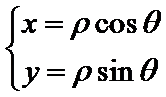
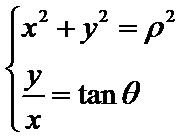
易错点
参数方程与普通方程的转化
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在极坐标系中,圆








正确答案
见解析。
解析
易求直线



依题意,有

知识点
在以






正确答案
3
解析
知识点
极坐标系中,极点到直线

正确答案
2
解析
略
知识点
在极坐标系中,圆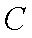
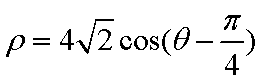
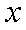
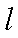
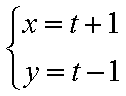
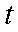

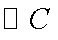
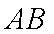
正确答案
见解析
解析
解: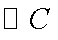
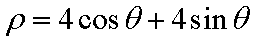

由
其圆心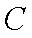
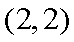

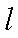
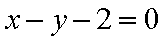
∴圆心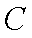
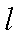
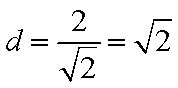
知识点
若曲线的极坐标方程为
正确答案

解析
做坐标系与参数方程的题,大家只需记住两点:1、


所以解析式为:
知识点
选修4—4:坐标系与参数方程
在极坐标系中,曲线




(1)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线
(2)求|BC|的长。
正确答案
见解析。
解析
解析:(1)由题意得,点

曲线L的普通方程为:
直线l的普通方程为:
(2)设B(


由韦达定理得

由弦长公式得
知识点
选修4-4:坐标系与参数方程(本小题满分10分)
选做题:
在直角坐标系







31.求曲线
32.若曲线




正确答案
对于曲线




正确答案
联立曲线






请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在极坐标系中,A为曲线ρ2+2ρcosθ﹣3=0 上的动点,B为直线ρcosθ+ρsinθ﹣7=0 上的动点,求AB 的最小值。
正确答案
见解析
解析
由ρ2+2ρcosθ﹣3=0,得:x2+y2+2x﹣3=0,即(x+1)2+y2=4。
所以曲线是以(﹣1,0)为圆心,以2为半径的圆。
再由ρcosθ+ρsinθ﹣7=0得:x+y﹣7=0。
所以圆心到直线的距离为d=
则圆上的动点A到直线上的动点B的最小距离为
知识点
在极坐标系中,已知直线




正确答案
见解析。
解析
直线的极坐标方程化为直角坐标方程为
圆的极坐标方程化为直角坐标方程为

因为截得的弦长为


即

知识点
扫码查看完整答案与解析