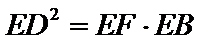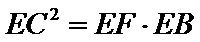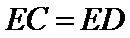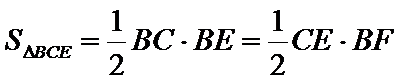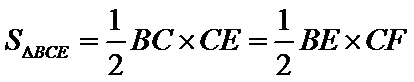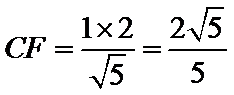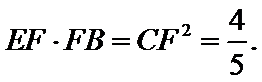- 选修部分
- 共638题
【选修4-1:几何证明选讲】
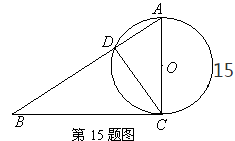
如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,
27.求证:BC=CD;
28.过点C作圆O的切线交AD延长线于点H,若AB=4,DH =1,求AD的长.
正确答案
(1)BC=CD;
解析
(1)由题意知

又∵



由


∴

∴


考查方向
解题思路
(1)通过弧长相等得出线段相等;(2)通过圆的切割线定理计算AD的长。
易错点
对圆的切割线定理的灵活运用。
正确答案
(2)AD=2
解析
(2)∵

又∵


∴


由(1)知


∴

由切割线定理,得


考查方向
解题思路
(1)通过弧长相等得出线段相等;(2)通过圆的切割线定理计算AD的长。
易错点
对圆的切割线定理的灵活运用。
4-1 :几何证明选讲








27.求证:

28.若


正确答案
(1)略;
解析
(Ⅰ)连结




而




而


考查方向
解题思路
先证明


易错点
不会做辅助线导致没有思路;
正确答案
(2)5
解析
(Ⅱ)连



设




考查方向
解题思路
先证明

易错点
不会利用圆的内接四边形的性质出错。
如图,








26.求
27.求证:
正确答案
(1)
解析
试题分析:本题属几何证明选讲中的切割线定理及相交弦定理,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,
(Ⅰ)由切割线定理知:



考查方向
解题思路
本题考几何证明选讲中的切割线定理及相交弦定理,解题步骤如下:(1)
利用切割线定理及三角形相似即可解出;(2)利用第一问及结合相交弦定理即可证明。
易错点
定理的使用不熟练。
正确答案
(2)见解析。
解析
试题分析:本题属几何证明选讲中的切割线定理及相交弦定理,(1)直接按照步骤来求(2)要注意对参数的讨论(3)涉及恒成立问题,转化成求函数的最值,
(Ⅱ)

考查方向
解题思路
本题考几何证明选讲中的切割线定理及相交弦定理,解题步骤如下:(1)
利用切割线定理及三角形相似即可解出;(2)利用第一问及结合相交弦定理即可证明。
易错点
定理的使用不熟练。
14.如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=_______.
正确答案
2
解析
首先由切割线定理得






考查方向
解题思路
平面几何问题主要涉及三角形全等,三角形相似,四点共圆,圆中的有关比例线段(相关定理)等知识,本题中有圆的切线,圆的割线,圆的相交弦,由圆的切割线定理和相交弦定理就可以得到题中有关线段的关系.
易错点
平面几何有关性质的综合应用
知识点
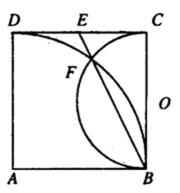
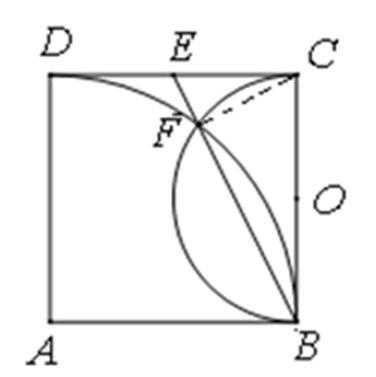
如图,正方形ABCD边长为2,以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结BF并延长交CD于点E.
27.求证:E为CD的中点;
28.求EF·FB的值.
正确答案
见解析
解析
解:(Ⅰ)由题可知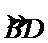
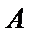
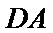
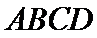
∴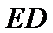
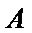
依据切割线定理得
∵圆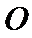
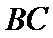
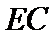
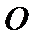
同样依据切割线定理得
故
∴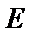
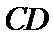
考查方向
解题思路
本题解题思路
1)借助圆的切割定理得出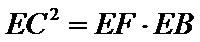
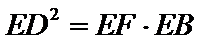
2)借助等面积求解FC,使用射影定理得到第二问
易错点
本题易错cd是两圆的切线,
正确答案
见解析
解析
解:
(Ⅱ)连结
∵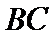
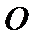
∴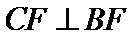
得
又在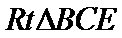
考查方向
解题思路
本题解题思路
1)借助圆的切割定理得出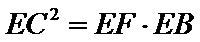
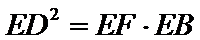
2)借助等面积求解FC,使用射影定理得到第二问
易错点
本题易错cd是两圆的切线,
选修4-1:几何证明选讲
如图,过圆













27.求
28.求
正确答案
3;
解析
延长











考查方向
解题思路
第一问由切割线定理可得;
易错点
三角形相似容易找错,切割线定理用不熟练。
正确答案
解析
过







考查方向
解题思路
第二问将两条线段归到两个相似三角形中,用相似得到比例关系。
易错点
三角形相似容易找错,切割线定理用不熟练。
8.如图,以











正确答案
解析
连接BE,由BC为直径知













考查方向
解题思路
1.先根据射影定理求出


易错点
1.看不出AB、BE和AE之间的关系;2.不会利用割线定理找关系求解。
知识点
已知AB是圆

求证:MN = MB;
求证:OC⊥MN。
正确答案
详见解题过程;
解析
试题分析:本题属于平面几何的基本问题,由圆的性质直接导出角关系
连结AE,BC,∵AB是圆O的直径,∴∠AEB=90°,∠ACB=90°∵MN=MC,
∴∠MCN=∠MNC又∵∠ENA=∠MNC,∴∠ENA=∠MCN∴∠EAC=∠DCB,
∵∠EAC=∠EBC,∴∠
考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
正确答案
详见解题过程
解析
试题分析:本题属于平面几何的基本问题,由角度等量关系去证所证。
设OC∩BE=F,∵OB=OC,∴∠OBC=∠OCB,由(1)知,∠MBC=∠MCB,∴∠DBM=∠FCM.又∵∠DMB=∠FMC,∴∠MDB=∠MFC,即∠MFC=90°∴OC⊥MN.
考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
选修4-1: 几何证明选讲.
如图所示,已知










28.求证:
29.若

正确答案
证明略
解析
∵



又∵


∴


又∵
考查方向
解题思路
先证明

易错点
找不准三角形相似或全等的条件
正确答案
PA=
解析
∵






∴


∴

考查方向
解题思路
先综合题中条件及28题中结论,解出EP=

易错点
找不准三角形相似或全等的条件
根据《城镇职工基本医疗保险定点零售药店管理暂行办法》,外配处方必须由
A.执业医师开具
B.定点零售药店执业药师开具
C.社区医护人员开具
D.定点医疗机构医师开具
E.定点零售药店药师开具
正确答案
D
解析
暂无解析
如图,弦AB与CD相交于O内一点E,过E作BC的平行线与AD的延长线交于点P,已知PD=2DA=2,则PE=__________.
正确答案
解析
∠C与∠A在同一个O中,所对的弧都是

知识点
如图,已知直角三角形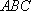
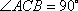
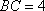

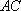

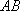
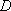
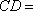
正确答案
解析
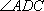
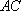
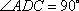
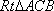
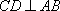
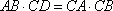
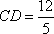
知识点
如图3,△ABC的外角平分线AD交外接圆于D,若
正确答案
解析
略
知识点
选修41:几何证明选讲
如图14,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明:
(1)BE=EC;
(2)AD·DE=2PB2.
正确答案
(1)连接AB,AC.由题设知PA=PD,
故∠PAD=∠PDA.
因为∠PDA=∠DAC+∠DCA,
∠PAD=∠BAD+∠PAB,
∠DCA=∠PAB,
所以∠DAC=∠BAD,从而BE=EC.
因此BE=EC.
(2)由切割线定理得PA2=PB·PC.
因为PA=PD=DC,所以DC=2PB,BD=PB.
由相交弦定理得AD·DE=BD·DC,
所以AD·DE=2PB2.
解析
(1)连接AB,AC.由题设知PA=PD,
故∠PAD=∠PDA.
因为∠PDA=∠DAC+∠DCA,
∠PAD=∠BAD+∠PAB,
∠DCA=∠PAB,
所以∠DAC=∠BAD,从而BE=EC.
因此BE=EC.
(2)由切割线定理得PA2=PB·PC.
因为PA=PD=DC,所以DC=2PB,BD=PB.
由相交弦定理得AD·DE=BD·DC,
所以AD·DE=2PB2.
知识点
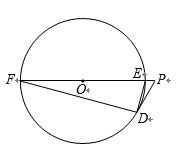
如图,已知直线PD切⊙O于点D,直线PO交⊙O于点E,F.若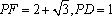
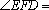
正确答案
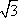
解析
略
知识点
扫码查看完整答案与解析