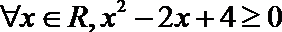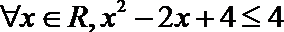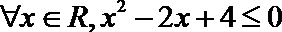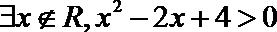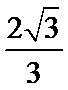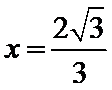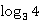- 直线和圆的方程
- 共1163题
15.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图;已知椭圆


(I)求椭圆C的方程;
(II)求
(III)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点。求证:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在

①函数


②
③函数


(Ⅰ)求函数
(Ⅱ)设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知数列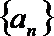
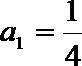
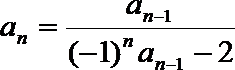
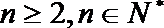
(Ⅰ)求数列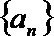
(Ⅱ)设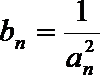
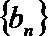
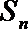
(Ⅲ)设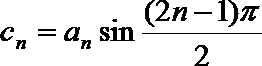
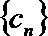
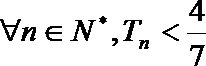
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知

正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
2.命题“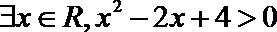
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知向量
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6 .若直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在△ABC中,已知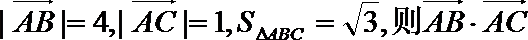
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在平面直角坐标系


及其上一点
⑴ 设圆





⑵ 设平行于





⑶ 设点





正确答案
(1)因为



则圆

又圆



则



⑵ 由题意得





则


解得




⑶ 



又
即

对于任意

此时


必然与圆交于


因此对于任意
综上
知识点
8.直线3x+4y=b与圆
正确答案
解析
∵直线


考查方向
解题思路
先确定圆的圆形,然后用点到直线的距离公式求解
易错点
圆的一般方程转换成标准方程换错,点到直线的距离求错
知识点
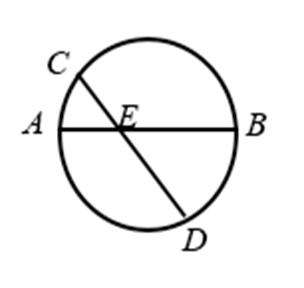
13.如图,AB是圆的直径,弦CD与AB相交于点E,BE=2AE=2,BD=ED,则线段CE的长为__________.
正确答案
解析
试题分析:设
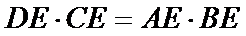
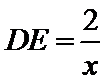


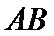


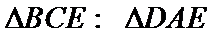
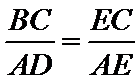
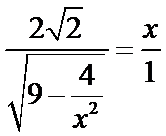
考查方向
解题思路
应用相交弦定理、切割线定理要抓住几个关键内容:如线段成比例与相似三角形、圆的切线及其性质、与圆有关的相似三角形等.本题根据相交弦定理即可求出CE长。
易错点
对相关定理不熟悉导致本题失分。
知识点
已知函数f(x)=x3+3ax2+3x+1.
(1)当
(2)若x∈[2,+∞)时,f(x)≥0,求a的取值范围。
正确答案
见解析。
解析
(1)当

f′(x)=3x2-
令f′(x)=0,得

当x∈(-∞,

当x∈(



当x∈(

(2)由f(2)≥0得
当
f′(x)=3(x2+2ax+1)≥

所以f(x)在(2,+∞)是增函数,于是当x∈[2,+∞)时,f(x)≥f(2)≥0.
综上,a的取值范围是
知识点
方程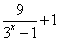
正确答案
解析
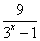
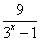
知识点
扫码查看完整答案与解析