- 直线和圆的方程
- 共1163题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在等差数列
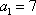
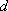

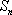
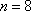
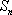
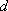
正确答案
解析
因为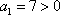
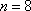
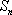

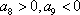
所以,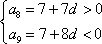
知识点
在极坐标系中,点(2,

正确答案
1
解析
根据极坐标和直角坐标的互化公式x=ρcosθ,y=ρsinθ,
可得点(2,

直线ρsin(θ﹣



故点(


知识点
抽样统计甲、乙两位设计运动员的5此训练成绩(单位:环),结果如下:
则成绩较为稳定(方差较小)的那位运动员成绩的方差为 。
正确答案
2
解析
易得乙较为稳定,乙的平均值为:
方差为:
知识点
已知向量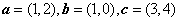
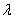
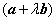

正确答案
解析
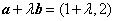
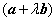
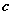
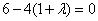
知识点
过抛物线




正确答案
解析

设



得:
知识点
函数
正确答案
[-1,0)∪(0,+∞)
解析
[-1,0)∪(0,+∞) 要使函数

∴定义域为[-1,0)∪(0,+∞)
知识点
3.行列式
正确答案
0.5
解析
考查行列式运算法则
知识点
设集合A={3,5,6,8},集合B={4,5, 7,8},则A∩B等于
正确答案
解析
集合A与集合B中的公共元素为5,8
知识点
某农场计划种植某种新作物,为此对这种作物的两个品种(分别称为品种甲和品种乙)进行田间试验,选取两大块地,每大块地分成n小块地,在总共2n小块地中,随机选n小块地种植品种甲,另外n小块地种植品种乙。
(1)假设n=2,求第一大块地都种植品种甲的概率;
(2)试验时每大块地分成8小块,即n=8,试验结束后得到品种甲和品种乙在个小块地上的每公顷产量(单位:kg/hm2)如下表:
分别求品种甲和品种乙的每公顷产量的样本平均数和样本方差;根据试验结果,你认为应该种植哪一品种?
正确答案
(1) 
解析
(1)设第一大块地中的两小块地编号为1,2,第二大块地中的两小块地编号为3,4,
令事件A=“第一大块地都种品种甲”.
从4小块地中任选2小块地种植品种甲的基本事件共6个;
(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).
而事件A包含1个基本事件:(1,2).
所以
(2)品种甲的每公顷产量的样本平均数和样本方差分别为:
品种乙的每公顷产量的样本平均数和样本方差分别为:
知识点
在△




正确答案
解析
略
知识点
设



正确答案
解析
不等式8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,则有Δ=(8sin α)2-4×8cos 2α=64sin2α-32cos 2α≤0,
即2sin2α-cos 2α=2sin2α-(1-2sin2α)=4sin2α-1≤0.
∴sin2α≤
∴
又0≤α≤π,结合下图可知,α∈
知识点
调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:
正确答案
0.254
解析
略
知识点
设双曲线









正确答案
解析
不妨令双曲线的方程为
又∵满足条件的直线只有一对,
∴tan 30°<

∴
∵b2=c2-a2,∴

∴

知识点
扫码查看完整答案与解析