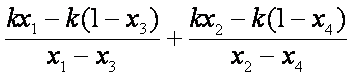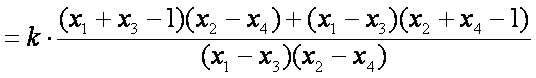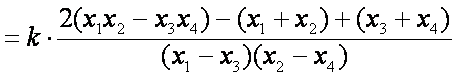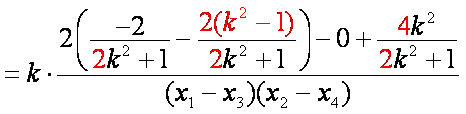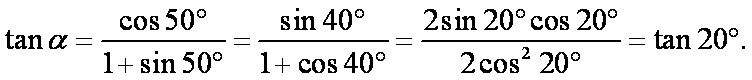- 直线和圆的方程
- 共1163题









(1)求
(2)若直线




正确答案
见解析。
解析
(1)设





∴


(2)由
∵直线

解得
当



,直线

当


知识点
某校高三年级在5月份进行一次质量考试,考生成绩情况如下表所示:
已知用分层抽样方法在不低于550分的考生中随机抽取5名考生进行质量分析,其中文科考生抽取了2名。
(1)求
(2)图6是文科不低于550分的6名学生的语文成绩的茎叶图,计算这6名考生的语文成绩的方差;
(3)已知该校不低于480分的文科理科考生人数之比为



正确答案
见解析。
解析
(1)依题意
(2)
∴这6名考生的语文成绩的方差
(3)依题意
解得
知识点
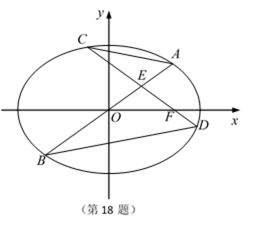
如图,在平面直角坐标系









(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点






正确答案
见解析。
解析
(1)由已知,得
所以椭圆的标准方程为
(2)设点


由已知,求得直线


又∵点

由①②,解得


所以点

(3)设


∵


∵


∵点


从而
所以
∴

知识点
如图,O为坐标原点,点A,B在⊙O上,且点A在第一象限,点

(1)求sin2θ的值;
(2) 若
正确答案
见解析
解析
(1) 因点C在


所以由三角函数定义知cosθ=
所以sin2θ=2sinθcosθ=
(2) 因为

所以
又∠

而

故点A的横坐标
知识点
已知圆



正确答案
解析
略
知识点
已知点



正确答案
解析
略
知识点
某中学为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用图1的条形图表示。根据条形图可得这50名学生这一天平均每人的课外阅读时间为
正确答案
解析
一天平均每人的课外阅读时间应为一天的总阅读时间与学生的比,
即
知识点
设函数










正确答案
① ② ④
解析
略
知识点
某旅游景点预计2013年1月份起前x个月的旅游人数的和p(x)(单位:万人)与x的关系近似地满足
(1)写出2013年第x月的旅游人数
(2)试问2013年第几月旅游消费总额最大,最大月旅游消费总额为多少元?
正确答案
见解析。
解析
(1)当

当


验证

(2)第
即
当



解得








当




综上,2013年第5月份的旅游消费总额最大,最大消费总额为3125万元. …12分
知识点
设





(1)求数列
(2)若

正确答案
见解析。
解析
(1)由已知得:

设数列



又



由题意得
故数列

(2)由(1)得



知识点
已知等比数列




正确答案
解析
由题可知



知识点
已知直线






正确答案
解析
由题意








知识点
如图,在平面直角坐标系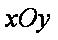
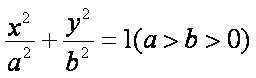
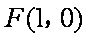
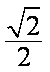
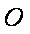
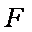
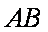
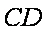
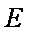
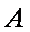
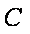
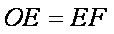
(1)求椭圆的方程;
(2)求证:直线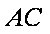
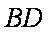
正确答案
见解析。
解析
(1)由题意,得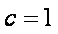
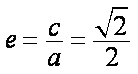
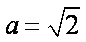
从而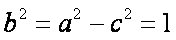
所以椭圆的方程为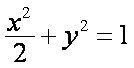
(2)证明:设直线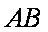
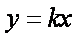
直线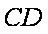
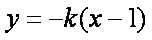
由①②得,点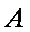
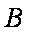
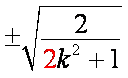
由①③得,点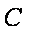
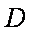
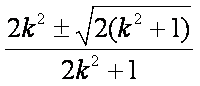
记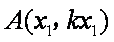
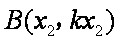
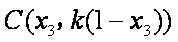
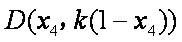
则直线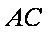
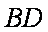
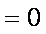
知识点
已知锐角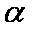
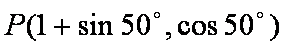
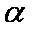
正确答案
解析
又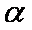
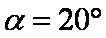
知识点
如图,已知PA是⊙O的切线,A是切点,直线PO交⊙O于B、C两点,D是OC的中点,连结AD并延长交⊙O于点E,若
(1)求∠AEC的大小;
(2)求AE的长。
正确答案
(1)60°(2)
解析
解析:
知识点
扫码查看完整答案与解析