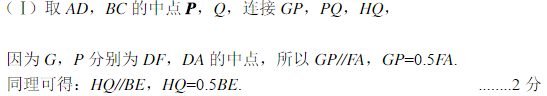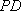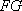- 直线和圆的方程
- 共1163题
点




正确答案
3
解析
略
知识点
(文)已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0,现给出如下结论:
①f(0)f(1)>0;②f(0)f(1)<0;③f(0)f(3)>0;④f(0)f(3)<0。
其中正确结论的序号是( )
正确答案
解析
设g(x)=x3-6x2+9x=0,则x1=0,x2=x3=3,其图象如下图:
要使f(x)=x3-6x2+9x-abc有3个零点,需将g(x)的图象向下平移,如图所示:
又f′(x)=3x2-12x+9=0时,x1=1,x2=3,即得f(1)是极大值,f(3)是极小值。
故由图象可知f(0)·f(1)<0,f(0)·f(3)>0。
知识点
如图,四边形ABCD是菱形,四边形MADN是矩形,平面MADN
(1)EF//平面MNCB;
(2)平面MAC
正确答案
见解析。
解析
知识点
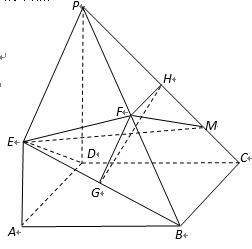
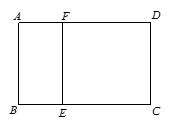
在如图所示的几何体中,四边形是ABEF长方形,DA⊥平面,ABEF,BC//AD,G,H分别为DF,CE的中点,且AD=AF=2BC。
(1)求证:GH//平面ABCD;
(2)求三棱锥与的体积之比。
正确答案
见解析。
解析
知识点
若某产品的直径长与标准值的差的绝对值不超过1mm 时,则视为合格品,否则视为不合格品。在近期一次产品抽样检查中,从某厂生产的此种产品中,随机抽取5000件进行检测,结果发现有50件不合格品。计算这50件不合格品的直径长与标准值的差(单位:mm), 将所得数据分组,得到如下频率分布表:
(1)将上面表格中缺少的数据填在答题卡的相应位置;
(2)估计该厂生产的此种产品中,不合格品的直径长与标准值的差落在区间(1,3]内的概率;
(3)现对该厂这种产品的某个批次进行检查,结果发现有20件不合格品。据此估算这批产品中的合格品的件数。
正确答案
见解析
解析
(1)
(2)不合格品的直径长与标准值的差落在区间(1,3]内的概率为
(3)合格品的件数为
知识点
一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是( )。
正确答案
解析
∵圆柱的三视图中有两个矩形和一个圆,
∴这个几何体不可以是圆柱
知识点
曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为( )
正确答案
解析
函数y=e-2x+1的导数为y′=-2e-2x,则y′|x=0=-2,曲线y=e-2x+1在点(0,2)处的切线方程是2x+y-2=0,直线y=x与直线2x+y-2=0的交点为

知识点
如图,菱形









(1)求证:

(2)求证:平面

(3)求三棱锥
正确答案
见解析
解析
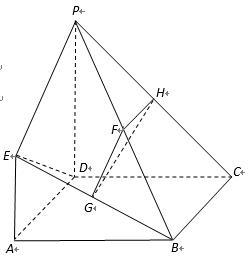
(1)证明:因为点

所以



所以


因为



所以

(2)证明:由题意,
因为


又因为菱形

因为
所以

因为

所以平面

(3)解:三棱锥

由(2)知,

所以



所求体积等于
知识点
已知直线


正确答案
解析
略
知识点
如图,在三棱柱








(1)求证:

(2)求证:

正确答案
见解析
解析
(1)连接




由












(2)∵平行四边形

∴
∵


∴
又∵




∴

知识点
如图,PA垂直于矩形ABCD所在的平面,
(1)求证:AF//平面PCE;
(2)求证:平面
(3)求四面体PEFC的体积.
正确答案
见解析。
解析
知识点
如图,已知四边形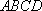
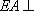

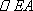

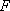
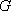
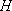
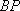
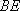
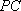
(1)求证:
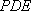
(2)求证:平面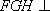
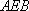
(3)在线段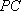
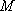
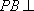
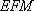
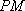
正确答案
见解析
解析
(1)证明:因为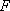
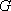
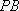
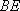
所以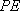
又因为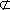
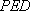


所以
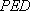
(2)因为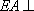

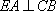
又因为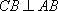
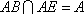
所以

由已知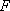
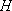
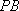
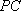
所以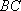
则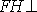
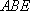
而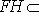
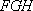
所以平面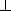
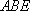
(3)在线段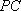
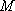
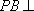
在直角三角形
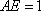
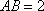
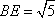
在直角梯形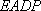
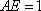
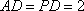
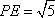
所以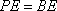
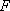
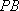

要使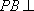
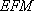
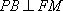
因为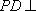
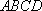
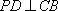
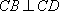
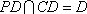
所以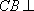
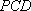
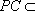
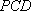
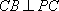
若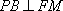
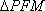
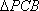
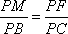
由已知可求得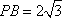
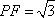
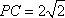

知识点
如图,直三棱柱ABC﹣A1B1C1中,△ABC是等边三角形,D是BC的中点。
(1)求证:直线A1D⊥B1C1;
(2)判断A1B与平面ADC1的位置关系,并证明你的结论。
正确答案
见解析
解析
(1)在直三棱柱ABC﹣A1B1C1中,AA1⊥面ABC,∴ AA1⊥BC,
在等边△ABC中,D是BC中点,∴ AD⊥BC
∵ 在平面A1AD中,A1A∩AD=A,∴BC⊥面A1AD
又∵ A1D⊂面A1AD,∴ A1D⊥BC
在直三棱柱ABC﹣A1B1C1中,四边形BCC1B1是平行四边形,∴ B1C1∥BC
∴ A1D⊥B1C1
(2) 在直三棱柱ABC﹣A1B1C1中,四边形ACC1A1是平行四边形,
在平行四边形ACC1A1中联结A1C,交于AC1点O,连接DO。
故O为A1C中点。
在三角形A1CB中,D 为BC中点,O为A1C中点,∴DO∥A1B。
因为DO⊂平面DAC1,A1B⊄平面DAC1,∴A1B∥面ADC1
∴ A1B与面ADC1平行。
知识点
如图4,在四棱锥





(1)求证:

(2)求证:
(3)若


正确答案
见解析。
解析
知识点
如图,矩形
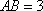
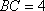
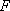
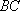
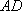
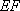
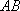
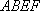
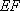

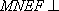
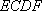
(1)求证: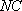

(2)若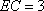
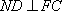
(3)求四面体
正确答案
见解析
解析
(1)证明:因为四边形
所以 
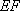

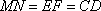
所以 四边形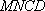
所以 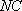
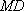
因为 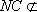
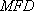
所以 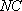
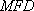
(2)证明:连接
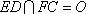
因为平面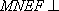
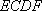
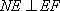
所以 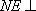
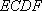
所以 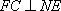
又 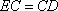
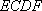
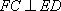
所以 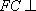
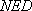
所以 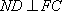
(3)解:设
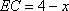
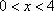
由(1)得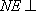
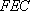
所以四面体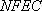
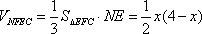
所以 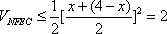
当且仅当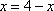
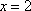
知识点
扫码查看完整答案与解析