- 直线和圆的方程
- 共1163题
如图,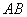
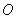
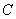
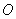
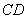
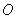
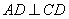
若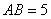
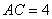
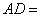
正确答案
解析
略
知识点
点P是以


正确答案
解析
略
知识点
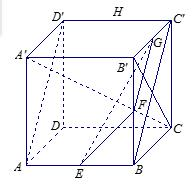
如图:













(1)求证:

(2)求证:

(3)求三棱锥
正确答案
见解析。
解析
解:(1)证明:依题


∴

(2)证明:

∴


∴
∴
∴


∴

(3)解:由题设知

∴

∴ 
知识点
直线
正确答案
解析
略
知识点
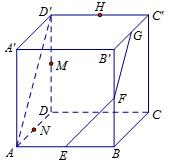
在正方体
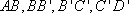
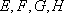
(1)求证: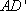
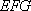
(2)求证:
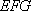
(3)判断点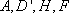
正确答案
见解析
解析
(1)证明:连接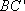
在正方体
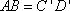
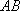
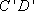
所以 四边形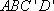
所以 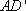
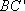
因为 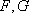
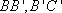
所以 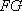

所以 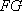

因为 
所以 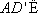
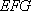
因为 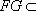
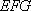
所以 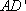
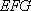
(2)证明:连接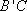
在正方体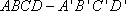
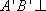
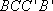
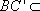

所以 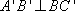
在正方形

因为 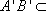
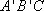
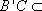
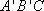
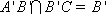
所以 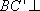

因为 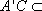
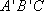
所以 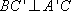
因为 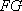
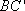
所以 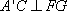
同理可证:
因为 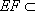
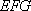
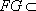
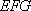
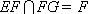
所以 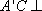

(3)点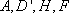
假设
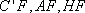
由(1)知,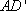
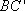
因为 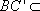
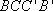
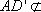
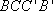
所以 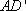
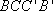
因为 
所以 平面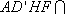
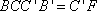
因为 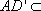
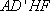
所以 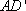

所以 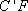
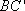
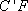
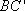
所以 点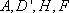
知识点
已知直线



①
③
正确答案
解析
略
知识点
已知菱形ABCD中,AB=4, 



(1)证明:BD //平面
(2)证明:
(3)当
正确答案
见解析
解析
(1)因为点


又





(2)在菱形



所以 在三棱锥

又
所以 

又 


(3)连结


所以 

因为 


又 

所以 



又 


因为 


知识点
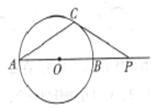
如图⊙O的直径AB=6cm,P是AB延长线上的一点,过P点作⊙O的切线,切点为C,连接AC,且∠CPA=30°,则BP=____
正确答案
3
解析
略
知识点
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,E,F分别是AB、PD的中点。
(1)求证:AF⊥平面PDC;
(2)求三棱锥B-PEC的体积;[来源:学*科*网]
(3)求证:AF∥平面PEC。
正确答案
见解析。
解析
知识点
在平面直角坐标系









正确答案
解析
略
知识点
已知一个半径为Im的半圆形工件,未搬动前如图所示(直径平行于地面放置),搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移40m,则圆心D所经过的路线长是 m。
正确答案
π+40
解析
略
知识点
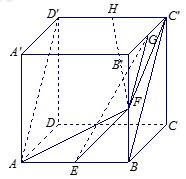
在如图所示的几何体中,四边形ABCD为矩形,EA⊥平面ABCD,EF// AB,AB=4,AE=EF =2。
(1)若G为BC的中点,求证:FG∥平面BDE;
(2)求证:AF⊥平面FBC。
正确答案
见解析。
解析
知识点
若一个底面是正三角形的三棱锥的俯视图如图所示,则其主视图与侧视图面积之比等于
正确答案
解析
设正三角形的边长


知识点
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=2,E,F分别是AB、PD的中点。
(1)求证:AF⊥平面PDC;
(2)求三棱锥B-PEC的体积;
(3)求证:AF∥平面PEC。
正确答案
见解析。
解析
知识点
正确答案
见解析。
解析
证明:(1)设AB中点为G,连结GE,GC。

又EG∥
又
又因为MN//AB,所以
而
(2)因为面

面

面
所以
所以D为
(3)因为EG//



所以


所以
又AB⊥CE,
所以

(3)
方法二(略证):过E点作

可用初中三角形相似或建立平面坐标系利用向量,直线斜率等
方法证明
又
所以
所以
所以
又
所以
知识点
扫码查看完整答案与解析