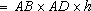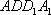- 直线和圆的方程
- 共1163题
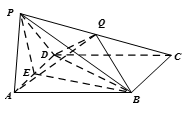
如图,四棱锥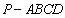
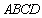
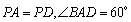
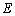
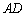
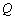
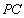
(1)求证: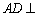
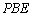
(2)若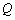
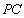
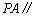
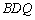
(3)若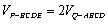
正确答案
见解析
解析
(1)证明:因为 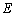
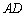
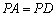
所以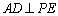
因为底面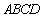
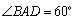
所以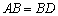
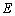
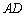
所以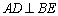
因为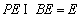
所以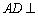
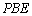
(2)证明:连接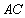
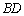
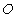
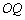
因为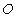
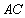
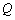
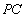
所以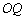
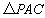
所以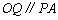
因为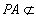
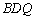
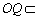
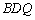
所以
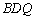
(3)解:设四棱锥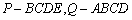
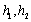
所以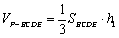
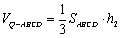
因为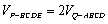

所以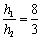
因为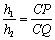
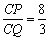
知识点
已知直线




正确答案
解析
略
知识点
如图4,过点P的直线与圆O相交于A,B两点,若PA=1,AB=2,PO=3,则圆O的半径等于_____________________.
正确答案
解析
知识点
过点

正确答案
解析
知识点
若直线



正确答案
解析
略
知识点
若直线

正确答案
解析
点


知识点
如图,点A、B、C都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为 。
正确答案
4.5
解析
∵过点C的切线交AB的延长线于点D,
∴DC是圆的切线,DBA是圆的割线,
根据切割线定理得到DC2=DB•DA,
∵AB=5,CD=6,
∴36=DB(DB+5)
∴DB=4,
由题意知∠D=∠D,∠BCD=∠A
∴△DBC∽△DCA,
∴
∴AC=
故答案为:4.5
知识点
如图,⊙O的直径AB=6cm,P是AB延长线上的一点,过p点作⊙O的切线,切点为C,连接AC,若∠CPA=30°,PC= cm。
正确答案
解析
连接OC,
PC是⊙O的切线,
∴∠OCP=90°
∵∠CPA=30°,OC=
∴tan30°=
即PC=
故填:
知识点
如图,三棱柱









(1)求证:

(2)在棱


1

正确答案
见解析。
解析
(1)证明:
取


又

在三棱柱








(2)设

部分的体积之比为1︰15,
则


所以符合要求的点
知识点
函数



正确答案
4
解析
略
知识点
已知椭圆












(1)求直线
(2)求
正确答案
(1)
解析
解析:(1)设直线

则有

又切点


所以直线

(2)设
由


又



所以
知识点
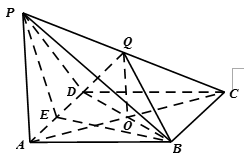
如图所示,圆柱的高为2,点A、B、C、D分别是圆柱下底面圆周上的点,ABCD为矩形,PA是圆柱的母线, AB=2,BC=4,E、F、G分别是线段PA,PD,CD的中点。
(1)求证:平面PDC
(2)求证:PB//面EFG;
(3)在线段BC上是否存在一点M,使得D到平面PAM的距离为2?若存
在,求出BM;若不存在,请说明理由。
正确答案
见解析。
解析
(1)∵PA是圆柱的母线,∴PA
∵CD

又∵ABCD为矩形,∴CD
而AD

又CD

(2)取AB中点H,连结GH,HE,
∵E,F,G分别是线段PA、PD、CD的中点,
∴GH//AD//EF,
∴E,F,G,H四点共面。
又H为AB中点,∴EH//PB。
又

∴PB//面EFG。
(3)
假设在BC上存在一点M,使得点D到平面PAM的距离为2,则以


由(2)知PA

∴VD—PAM=

∵
∴
∵VD—PAM =
∴

∵
∴在BC上存在一点M,当
知识点
如图1,在正三角形ABC中,AB=3,E、F、P分别是AB、AC、BC边上的点,AE=CF=CP=1。将


(1)求证:PF//平面A1EB;
(2)求证:平面
(3)求四棱锥A1—BPFE的体积。
正确答案
见解析。
解析
(1)证明:∵
又∵





(2)法一:由图1,∵
∴
∵

∵平面





∴
∵


法二:由图1,∵
∴
∵
∴在图2中,
∵

∵


(3)由(1)(2)可知,四边形




∵

∴四棱锥
知识点
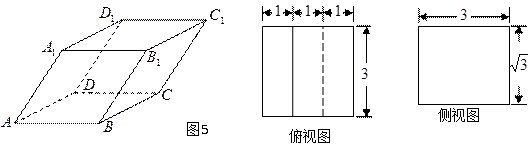
如图5,已知四棱柱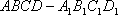


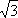
(1)求该四棱柱的体积;
(2)取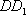
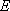
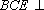
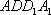
正确答案
见解析。
解析
(1)依题意,四棱柱的底面是矩形,侧面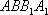
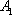
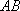
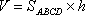
(2)连接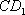

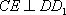
又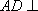

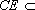
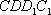

因为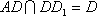
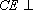
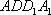
因为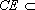
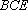
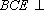
知识点
四边形ABCD内接于⊙O,BC是直径,MN切⊙O于A,∠MAB=25•,则∠D= 。
正确答案
115°
解析
连接BD,AC,根据弦切角定理∠MAB=∠ACB=∠ADB=25°
∵∠D所对的弧是
∴∠D=∠ADB+∠BDC
∴所求角度为25°+90°=115°
故答案为:115°
知识点
扫码查看完整答案与解析