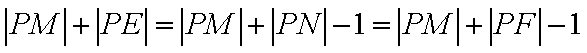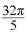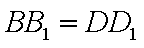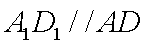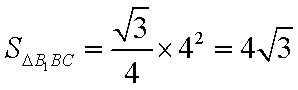- 直线和圆的方程
- 共1163题
如图,









(1) 证明:
(2)求四棱锥

(3)若


正确答案
见解析
解析
(1)如图,连接





又






又
(2)如图,连接











即

设圆柱高为



(3)如图,作过



















知识点
若直线


正确答案
解析
由





知识点
如图,在平面直角坐标系xOy中,已知椭圆E:

(1)求直线OP的方程;
(2)求
(3)设a为常数,过点O作两条互相垂直的直线,分别交椭圆于点B、C,分别交圆A点M、N,记三角形OBC和三角形OMN的面积分别为S1,S2,求S1S2的最大值。
正确答案
见解析
解析
(1)连结A2P,则A2P⊥A1P,且A2P=a,
又A1A2=2a,所以∠A1A2P=60°。
又A2P=A2O,所以△OPA2为正三角形,
所以∠POA2=60°,
所以直线OP的方程为
(2)由(1)知,直线A2P的方程为

联立①②解得
因为



故椭圆E的方程为
由

所以


(3)不妨设OM的方程为y=kx(k>0),
联立方程组

所以
用

同理可得,

所以
因为
当且仅当k=1时等号成立,
所以S1•S2的最大值为
知识点
已知


正确答案
18
解析
因为



知识点
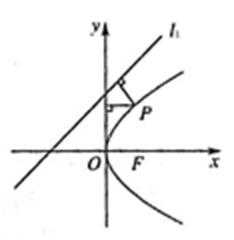
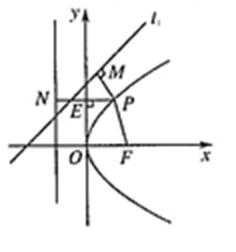
已知直线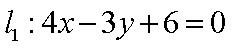
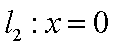
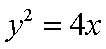
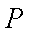
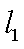
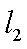
正确答案
1
解析
如图所示,作抛物线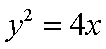
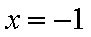
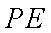
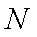
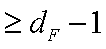
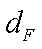
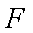
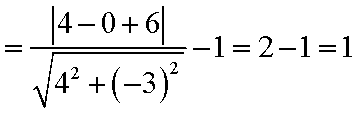
知识点
一容量为20的样本数据,分组后,组距与频数如下:[10,20],2;(20,30],3;(30,40],4;(40,50],5;(50,60],4;(60,70],2.则样本在(10,50]上的频率是 。
正确答案
0.7
解析
由题意知样本容量n=20,
(10,50]上的频数为m=2+3+4+5=14,
则频率是
知识点
如图所示,四棱锥



(1)若



(2)若

(3)在(2)的条件下,若

正确答案
见解析
解析
(1)证明:连结


因为底面


因为 


因为



所以

(2)证明:因为底面
所以


因为

因为




所以 
(3)因为

因为


由(2)知

所以



因为四边形是边长为2的菱形,且
所以
所以
知识点
已知椭圆C的中心在原点,对称轴为坐标轴,且过
(1)求椭圆C的方程
(2)直线

正确答案
见解析。
解析
(1)设椭圆C 的方程为
由椭圆C过点
解得

(2)设
消去y整理得
由

而
故
知识点
已知实数x,y满足
正确答案
1
解析
∵ 变量x,y满足约束条件
目标函数为:x2+y2﹣2x的几何意义,
可行域内的点到(1,0)距离的平方减1;
点到直线的距离公式可得:
x2+y2﹣2x的最小值为:(
故答案为:1。
知识点
蒸汽机飞轮的直径为1.2米,以320(转/分)的速度作逆时针旋转,则飞轮上一点1秒内所经
过的路程为 ▲ 米。
正确答案
解析
飞轮上一点1秒内所经过的路程为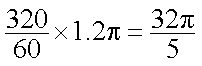
知识点
在如图的多面体中,









(1)求证:

(2)求证:
(3)求多面体
正确答案
见解析。
解析
(1)证明:∵

又∵



∴四边形

∵





(2)证明:∵




又




过





∵


∵


∴



又





∵


(3)∵




由(2)知四边形

∴
知识点
如图1,





(1)证明:
(2)设







正确答案
见解析
解析
(1)∵











(2)连接





∵














知识点
已知直线ax+by﹣1=0(a,b不全为0)与圆x2+y2=50有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有( )
正确答案
解析
解:当x≥0,y≥0时,圆上横、纵坐标均为整数的点有(1,7)、(5,5)、(7,1),
根据题意画出图形,如图所示:
根据圆的对称性得到圆上共有3×4=12个点横纵坐标均为整数,
经过其中任意两点的割线有C122=66条,过每一点的切线共有12条,
上述直线中经过原点的有6条,如图所示,
则满足题意的直线共有66+12﹣6=72条。
知识点
如图,在棱长均为4的三棱柱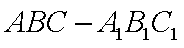
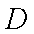
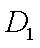
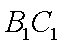
(1)求证: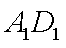
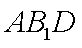
(2)若平面ABC⊥平面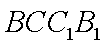
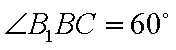
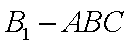
正确答案
见解析
解析
(1)证明:
如图,连结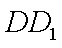
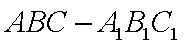
因为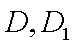

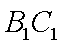
所以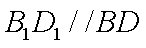

所以四边形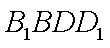
所以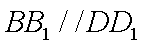
又因为
所以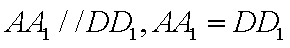
所以四边形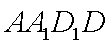
又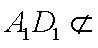
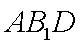
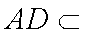
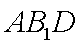

(2)在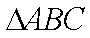
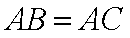
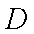

因为平面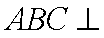
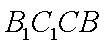

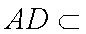
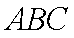
所以
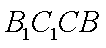
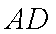
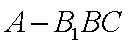
在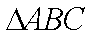
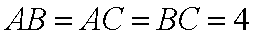
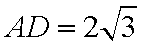
在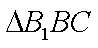
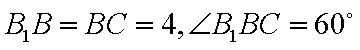
所以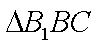
所以三棱锥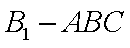
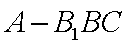
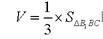
知识点
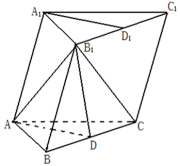
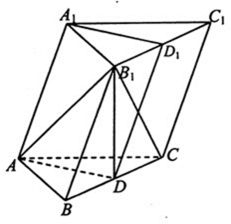
如图,棱柱ABCD—A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°。
(1)证明:BD⊥AA1;
(2)在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
正确答案
见解析。
解析
(1)在A1作A1O⊥AC于点O,由于平面AA1C1C⊥平面ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD,
又底面为菱形,所以AC⊥BD
(2)
存在这样的点P,连接B1C,因为A1B1

∴四边形A1B1CD为平行四边形。∴A1D//B1C
在C1C的延长线上取点P,使C1C=CP,连接BP
因B1B
∴BB1
则BP//B1C ∴BP//A1D ∴BP//平面DA1C1
知识点
扫码查看完整答案与解析