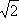- 直线和圆的方程
- 共1163题
12.过点






正确答案
解析
有割线定理得,(PC-


设A(x,y),则(x+4)2+y2=10与圆
x=-1, y=


考查方向
解题思路
直线与圆相交的问题,常常考查求弦长问题,涉及到弦的中点即可使用圆的相关的几何性质,转化为直线垂直,进而求出斜率,使用点斜式求出方程。
易错点
1、本题点

2、两直线垂直的等价条件不能与直线的斜率联系起来。
知识点
14. 已知过点



正确答案
【答案】x-3y-6=0 ,
解析
由已知可得圆的半径为5,而弦长刚好等于直径,所以直线经过圆心,由直线方程的两点式方程可以求出直线的方程为x-3y-6=0。
考查方向
解题思路
本题可以将已知条件转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去利用勾股定理算出圆心到直线的距离,然后利用点到直线的距离构造一个关于斜率的方程解出即可。
易错点
本题不知道将已知转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去求解。
知识点
5. 经过抛物线x2=4 y的焦点和双曲线-=1的右焦点的直线方程为( )
正确答案
解析
抛物线的焦点坐标是(0,1),双曲线的焦点是(5,0),两点式方程写出所求直线的方程再化为直线方程的一般式可得D选项。
考查方向
解题思路
求出抛物线的焦点和双曲线的焦点坐标,然后用两点式方程求出即可。
易错点
1、容易求错抛物线的焦点坐标。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
双曲线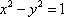
正确答案
解析
本题考查的是双曲线的性质,因为双曲线的两个顶点到两条渐近线的距离都相等,故可取双曲线的一个顶点为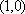
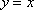
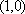
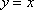
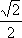
知识点
定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线C1:y=x2+a到直线l:y=x的距离等于曲线C2:x2+(y+4)2=2到直线l:y=x的距离,则实数a=__________。
正确答案
解析
x2+(y+4)2=2到直线y=x的距离为


知识点
抛物线

正确答案
解析
略
知识点
4.过点



正确答案
解析
本题考查了利用截距式求直线方程这个知识点分两种情况:①当截距不为0时,设在x轴上的截距为a,则在y轴上的截距为2a,所以直线方程为

考查方向
本题主要考查了求直线方程这个知识点,是高考C级考点之一,几乎是高考必考内容,属于基础题,体现了学生对基础知识的掌握情况.求直线方程通常有下面几种方法:
①点斜式;②斜截式;③两点式;④截距式;⑤一般式。
易错点
本题易忽视截距为0这种情况,导致少一个答案 .
知识点
20. 椭圆C的对称中心是原点,对称轴是坐标轴,离心率与双曲线

(1)求出椭圆方程;
(2)一条纵截距为2的直线l1与椭圆C交于P,Q两点,若以PQ直径的圆恰过原点,求出直线方程;
(3)直线l2:

正确答案
(1)
(2)
(3)不存在直线
解析
试题分析:本题直线与圆锥曲线的综合应用问题,解析如下:
解: (1)双曲线
所以椭圆的离心率为
设椭圆的长半轴为

半焦距为
所以
所以
设椭圆的方程为

所以
所以椭圆的标准方程为
(2)直线

设直线为

得:
由



以

①即
也即
即
将①式代入,得
即
解得
所以
(3)由方程组
得
设
则
所以
因为直线
所以

则

考查方向
本题考查了求椭圆的标准方程,直线与圆锥曲线的位置关系等知识点,属于拔高题。
易错点
利用已知条件整理容易出错。
知识点
13.已知过点

正确答案

解析
考查方向
解题思路
1、设直线方程(注意斜率不存在的情况)
2、使用弦长公式求出圆心到直线的距离
3、使用点到直线的距离公式计算圆心到直线的距离求出k并得出最终结果
易错点
本题易于在设直线方程忽略斜率不存在的情况,导致漏解
知识点
设曲线C的方程为(x-2)2+(y+1)2=9,直线l的方程x-3y+2=0,则曲线上的点到直线l的距离为
正确答案
解析
略
知识点
在平面直角坐标系xoy中,直线l的参数方程是



正确答案
2
解析
略
知识点
在极坐标系中,圆
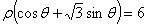
正确答案
1
解析
略
知识点
设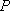
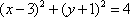
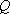
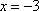
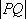
( )
正确答案
解析
略
知识点
若点


正确答案
解析
略
知识点
扫码查看完整答案与解析