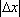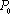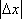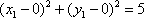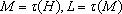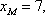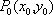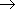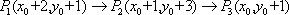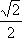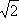- 直线和圆的方程
- 共1163题
14．若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3.在平面直角坐标系中，设C1={(x，y)|(x－2)2+(y－3)2=1}，C2={(x，y)|(x－3)2+(y－4)2=9}，且M∈C1，N∈C2，P为x轴上的动点，则|PM|+|PN|的最小值为（ ）
A5
B
C6－2
D
正确答案
解析
设P(x，0)，C1区域的圆心C1为(2，3)，C2区域的圆心C2为(3，4)
设C1(2，3)关于x轴的对称点为C1'(2，-3)，
那么|PC1|+|PC2|=|PC1'|+|PC2|≥|C1'C2|=
所以|PM|+|PN|=|PC1|+|PC2|-4≥5
知识点
9.函数f(x)=
A
B4
C
D5
正确答案
解析
f(x)=
其几何意义是x轴上的动点P(x，0)到两定点M(1，2)和N(-3，1)的距离之和(如图)
N关于x轴的对称点为N'(-3，-1)，
易知当M，N'，P三点共线(即P在线段MN上)时，f(x)取得最小值，
f(x)min=|MN'|= 
知识点
设D为不等式组
正确答案
解析
区域D表示的平面部分如图阴影所示：
根据数形结合知(1,0)到D的距离最小值为(1,0)到直线2x－y＝0的距离
知识点
规定函数
①函数
②函数
③若函数
以上命题是真命题的是：
正确答案
解析
知识点
已知点
A
B
C
D
正确答案
解析
略
知识点
设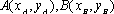
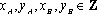
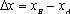
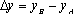
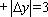
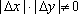
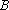
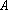
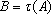
（1）请问：点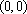
（2）已知点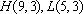
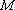
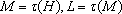
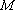
（3）已知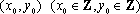
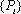
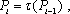
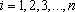
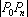
正确答案
见解析
解析
（1）因为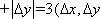
故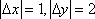
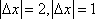
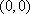
所以这些可能值对应的点在以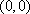
（2）设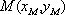
所以有
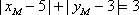
所以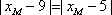
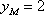
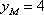
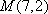
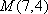
（3）当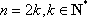
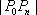
当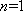
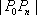
当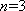
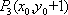
故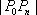
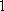
当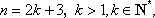
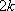
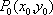
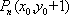
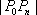
综上，当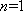
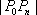
当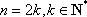
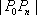
当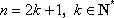
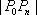
知识点
7.抛物线
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
14．如果
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知圆心为（2，0）的圆C与直线y=x相切，求切点到原点的距离 ( )
A1
B
C2
D
正确答案
解析
先画图由相切得圆心到直线的距离就是半径长，再用勾股定理计算出切点到原点的距离为
考查方向
解题思路
由相切求出半径长，再用勾股定理计算
易错点
相切关系的刻画
知识点
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
双曲线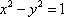
A
B
C1
D
正确答案
解析
本题考查的是双曲线的性质，因为双曲线的两个顶点到两条渐近线的距离都相等，故可取双曲线的一个顶点为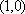
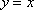
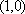
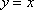
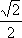
知识点
定义：曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离，已知曲线C1：y＝x2＋a到直线l：y＝x的距离等于曲线C2：x2＋(y＋4)2＝2到直线l：y＝x的距离，则实数a＝__________。
正确答案
解析
x2＋(y＋4)2＝2到直线y＝x的距离为
知识点
抛物线
正确答案
解析
略
知识点
在极坐标系中，圆
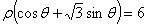
正确答案
1
解析
略
知识点
扫码查看完整答案与解析