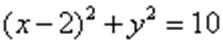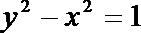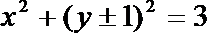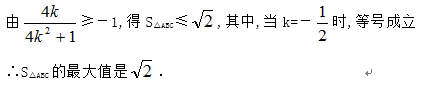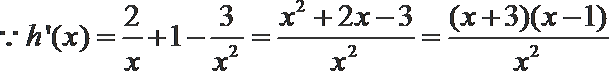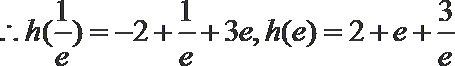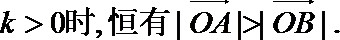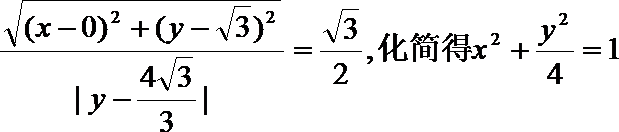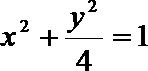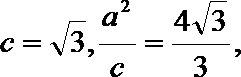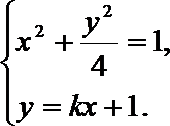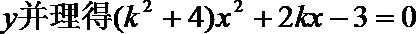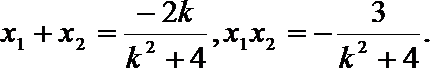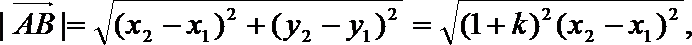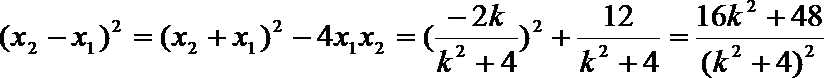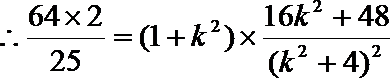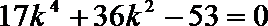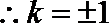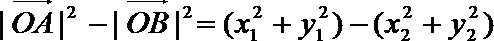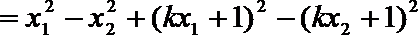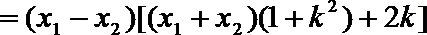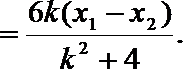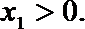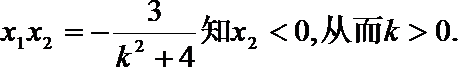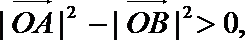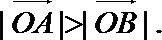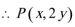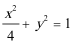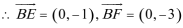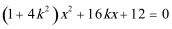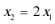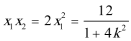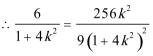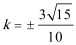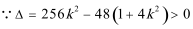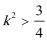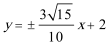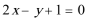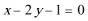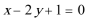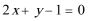- 直线和圆的方程
- 共1163题
13.已知圆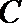
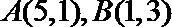

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系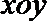
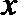
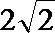
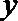
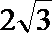
(I)求圆心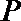
(II)若点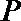
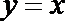
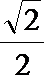
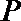
正确答案
(Ⅰ)
(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
22.已知在平面直角坐标系xOy中的一个椭圆,它的中心在原点,左焦点为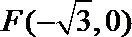
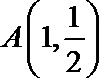
(1)求该椭圆的标准方程;
(2)过原点O的直线交椭圆于点B,C,求△ABC面积的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点,那么,当小圆这样滚过大圆内壁的一周时,点M,N在大圆内所绘出的图形大致是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知动圆过定点A(0,2), 且在x轴上截得的弦长为4。
(1) 求动圆圆心的轨迹C的方程;
(2)点P为轨迹C上任意一点,直线l为轨迹C上在点P处的切线,直线l交直线:y=-1于点R,过点P作PQ⊥l交轨迹C于点Q,求△PQR的面积的最小值。
正确答案
(1)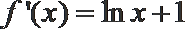
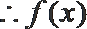
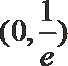
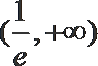
①当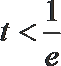
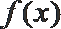
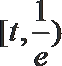
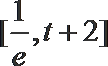
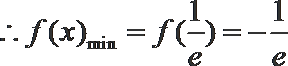
②当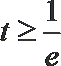
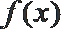
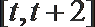
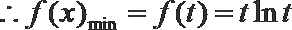
(2)由题意可知,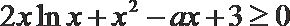
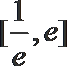
即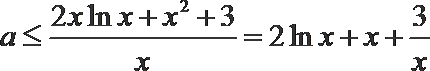
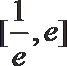
令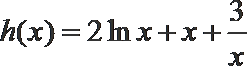
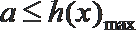
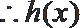
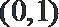
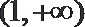
则在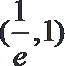
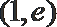
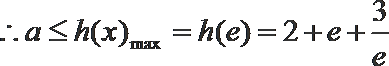
解析
解析已在路上飞奔,马上就到!
知识点
16.与直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知圆


(1)设
(2)若

正确答案
解(1)
即
由

(2)设
所以
解析
解析已在路上飞奔,马上就到!
知识点
18.已知:以点





(1)求证:
(2)设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.在平面直角坐标系xoy中,动点P到定点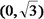
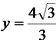
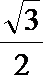
(I)写出C的方程;
(II)设直线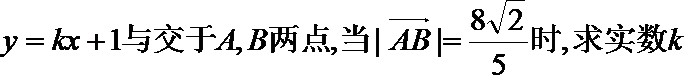
(III)若点A在第一象限,证明:当
正确答案
解:(I)设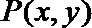
故曲线C的方程为
注:若直接用
得出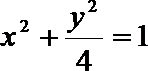
(II)设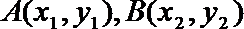
消去
故
而
化简整理得
解得: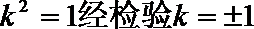
(III)
因为A在第一象限,故
由
故
即在题设条件下,恒有
解析
解析已在路上飞奔,马上就到!
知识点
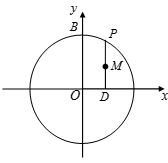
12.已知圆











正确答案

解析
解析已在路上飞奔,马上就到!
知识点
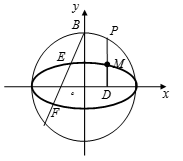
19.如图,圆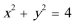
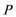
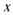
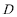
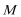
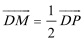
(1)求动点
(2)过点
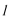
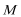
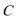
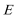
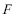
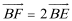
正确答案
(1)设轨迹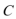
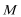

则由题意得: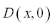
则
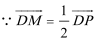
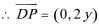

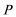
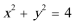
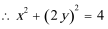
即动点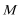
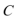
(2)当直线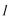
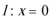
此时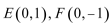
显然不满足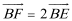
因此直线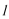
设直线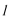
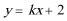
代入椭圆方程,
可得:
设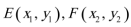
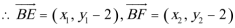
由题意知:
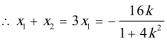
解此方程可得:
解得:
显然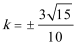

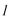
解析
解析已在路上飞奔,马上就到!
知识点
8.若函数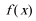
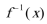
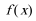
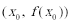
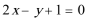
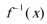
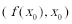
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,直线l :y=x+b与抛物线C :x2=4y相切于点A。
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程。
正确答案
(1)由


因为直线与抛物线C相切
所以
解得
(2)由(1)可知
故方程(
解得
得y=1
故点A(2,1)
因为圆A与抛物线C的准线相切
所以圆心A到抛物线C的准线y=-1的距离等于圆A的半径r
即r=|1-(-1)|=2
所以圆A的方程为
解析
解析已在路上飞奔,马上就到!
知识点
11.已知圆

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析