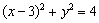直线和圆的方程_章节学习

1

题型：填空题

|

填空题 · 5 分

13.已知圆，过圆心的直线交圆于两点，交轴于点. 若恰为的中点，则直线的方程为 .

正确答案

或。

解析

由｜PA｜＝｜PB｜

则｜AC｜＝｜PA｜，即 A是PC的三等分点

xA＝2，代入圆方程5

即 A(2，3)或(2，7)，故直线l 的方程为：或

故此题答案为或。

考查方向

本题主要考查直线与圆综合应用及圆锥曲线中的“型问题”等知识，意在考查考生数形结合思想解决问题的能力，在近几年的各省高考题出现的频率较高，常在直线与圆锥曲线等知识点处交汇命题，较难。

解题思路

由｜PA｜＝｜PB｜则｜AC｜＝｜PA｜，即 A是PC的三等分点，得xA＝2；把xA＝2，代入圆方程5得到 A(2，3)或(2，7)，再得直线方程。

易错点

本题在“恰为的中点”的应用上易出错。

知识点

圆的切线方程

1

题型：简答题

|

多选题

依据《中华人民共和国招标投标法》，联合体投标需遵循的规定有( )。

A．联合体各方应按招标文件提供的格式签订联合体协议书，明确联合体牵头人和各方权利义务
B．联合体投标的，应当以联合体各方或者联合体中牵头人的名义提交投标保证金
C．联合体各方签订共同投标协议后，可以再以自己的名义单独投标
D．由同一专业的单位组成的联合体，按照资质等级较高的单位确定资质等级
E．联合体各方签订共同投标协议后，不得组成新的联合体或参加其他联合体在同一项目中投标

正确答案

A,B,E

解析

暂无解析

1

题型：填空题

|

填空题 · 5 分

在平面直角坐标系中，圆的方程为，若直线

上至少存在一点，使得以该点为圆心，1为半径的圆与圆有公共点，则的最大值是。

正确答案

。

解析

∵圆C的方程可化为：，∴圆C的圆心为，半径为1。

∵由题意，直线上至少存在一点，以该点为圆心，1为半径的圆与圆有公共点；

∴存在，使得成立，即。

∵即为点到直线的距离，∴，解得。

∴的最大值是。

知识点

直线与圆的位置关系

1

题型：填空题

|

填空题 · 5 分

过点（-1,2）的直线l被圆截得的弦长，则直线l的斜率为__________。

正确答案

1或

解析

由题意，直线与圆要相交，斜率必须存在，设为，则直线的方程为.又圆的方程为，圆心为，半径为1，所以圆心到直线的距离，解得

知识点

直线与圆的位置关系

1

题型：单选题

|

单选题 · 5 分

直线被圆截得的弦长为

A1

B2

C4

D

正确答案

C

解析

圆心，圆心到直线的距离，半径，所以最后弦长为.

知识点

直线与圆的位置关系

1

题型：填空题

|

填空题 · 4 分

已知圆C过点（1,0），且圆心在x轴的正半轴上，直线l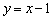：被该圆所截得

的弦长为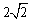，则圆C的标准方程为 .

正确答案

解析

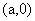
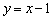
由题意，设圆心坐标为，则由直线l：被该圆所截得

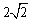
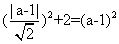
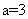
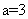
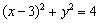
的弦长为得，，解得或-1，又因为圆心在x轴的正半轴上，所以，故圆心坐标为（3，0），又已知圆C过点（1,0），所以所求圆的半径为2，故圆C的标准方程为。

知识点

直线与圆的位置关系直线与圆相交的性质

1

题型：填空题

|

填空题 · 5 分

过直线x＋y－＝0上点P作圆x2＋y2＝1的两条切线，若两条切线的夹角是60°，则点P的坐标是__________。

正确答案

解析

如图所示，过点P作圆x2+y2=1的两条切线，切点分别为A，B，

由已知得，∠APO=30°，

所以|PO|=2.

设P点坐标为(x0，y0)，

则解得

故所求点P坐标为。

知识点

直线与圆的位置关系

1

题型：单选题

|

单选题 · 5 分

已知圆，过点的直线，则（）

A与相交

B与相切

C与相离

D以上三个选项均有可能

正确答案

A

解析

因为点P（3,0）在圆的内部，所以过点P的直线必与圆相交.选A.

知识点

直线与圆的位置关系

1

题型：单选题

|

单选题 · 5 分

过点P(1,1)的直线将圆形区域{(x，y)|x2＋y2≤4}分为两部分，使得这两部分的面积之差最大，则该直线的方程为(　　)

Ax＋y－2＝0

By－1＝0

Cx－y＝0

Dx＋3y－4＝0

正确答案

A

解析

当OP与该直线垂直时，符合题意；此时kOP＝1，故所求直线斜率k＝－1.又已知直线过点P(1,1)，因此，直线方程为y－1＝－(x－1)，即x＋y－2＝0.

知识点

直线的一般式方程直线与圆的位置关系直线与圆相交的性质

1

题型：简答题

|

简答题 · 10 分

，在极坐标中，已知圆经过点，圆心为直线与极轴的交点，求圆的极坐标方程。

正确答案

解析

∵圆圆心为直线与极轴的交点，

∴在中令，得。

∴圆的圆心坐标为（1，0）。

∵圆经过点，∴圆的半径为

。

∴圆经过极点。∴圆的极坐标方程为。

知识点

直线与圆的位置关系点的极坐标和直角坐标的互化

1

题型：单选题

|

单选题 · 5 分

将圆x2＋y2－2x－4y＋1＝0平分的直线是(　　)

Ax＋y－1＝0

Bx＋y＋3＝0

Cx－y＋1＝0

Dx－y＋3＝0

正确答案

C

解析

圆x2＋y2－2x－4y＋1＝0可化为标准方程

(x－1)2＋(y－2)2＝4，要使直线平分此圆，则直线需过圆心(1,2)，代入检验，C项满足条件，故选C

知识点

直线与圆的位置关系

1

题型：单选题

|

单选题 · 5 分

已知点M(a,b)在圆外, 则直线ax + by = 1与圆O的位置关系是（）

A相切

B相交

C相离

D不确定

正确答案

B

解析

点M(a, b)在圆

=圆的半径，故直线与圆相交。

知识点

直线与圆的位置关系

1

题型：单选题

|

单选题 · 5 分

已知，则直线与圆：的位置关系是

A相交

B相切

C相离

D不能确定

正确答案

B

解析

略

知识点

直线与圆的位置关系

1

题型：填空题

|

填空题 · 5 分

设上的两个随机数，则直线没有公共点的概率是 ▲ .

正确答案

解析

略

知识点

直线与圆的位置关系与长度、角度有关的几何概型

1

题型：填空题

|

填空题 · 5 分

若圆心在直线上、半径为的圆与直线相切，则圆的方程是_____.

正确答案

或

解析

略

知识点

圆的标准方程直线与圆的位置关系

热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点