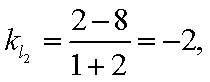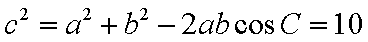- 直线和圆的方程
- 共1163题
如图,已知椭圆



(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线

[来源:学§科§网]
正确答案
见解析
解析
(1)设点E(m,m),由B(0,-2)得A(2m,2m+2)。
代入椭圆方程得

解得

所以A(

故直线AB的方程为
(2)设


设

∴
又点M在直线y=x上,解得M点的横坐标
设

∴
点N在直线y=x上,,解得N点的横坐标
所以OM·ON=

=


知识点
已知直线2x+y-c=0与圆x2+y2

正确答案
解析
略
知识点
在四棱锥


(1)求证: PD⊥平面PAB;
(2)设E是棱AB的中点,

求四棱锥
正确答案
见解析
解析
(1)证明:因为平面PAD⊥平面ABCD,平面PAD

所以
又
又PD⊥PB,所以PD⊥平面PAB
(2)设
在Rt△PAE中,
在Rt△BEC中,
在Rt△BEC中,
由


所以四棱锥
故四棱锥
知识点
点
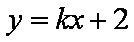




正确答案
-1或1
解析
略
知识点
已知直线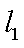
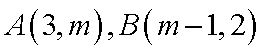
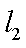
(1)当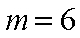
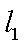

(2)若

正确答案
见解析
解析
解析:(1)当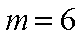


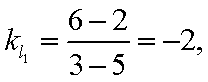
故 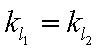
此时,直线
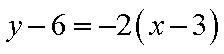

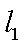
从而,
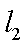
(2)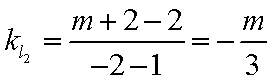

若
当

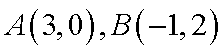

不符合题意,舍去;……………………………………………………………………..7分
当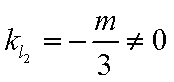



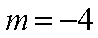
综上:
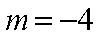
知识点
已知圆










(1)求直线
(2)求圆
正确答案
(1)
解析
解析:(1)由题意知:直线

故直线

(2)根据题意设: 


圆





解得:

圆

圆

知识点
如图,已知AB为圆O的一条直径,以端点B为圆心的圆交直线AB于C、D两点,交圆O于E、F两点,过点D作垂直于AD的直线,交直线AF于H点。
(1)求证:



(2)若AC=2,AF=2 ,求
正确答案
见解析
解析
解析:(1)因为


又
故




所以,



(2)因为





所以
又
则

连接





知识点
已知斜三棱柱ABC-A1 B1C1,所有棱长 均为2,若点A1在底面ABC的射影落在AB的中点上。
(1)在线段A1C1上找到一点N,使得MN∥面B1C1CB,求A1iN的长度;
(2)求四棱锥体积VA—BB1C1C。
正确答案
见解析
解析
(1)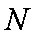

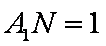
理由如下:取
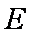
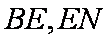

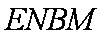

(2)

知识点
一个小组的3个学生在分发数学作业时,从他们3人的作业中各随机地取出2份作业,则每个学生拿的都不是自己作业的概率是
正确答案
解析
略
知识点
已知椭圆E:
原点对称的两点,且直线PA的斜率与直线

(1)求E的方程;
(2)过E的右焦点作直线l与E交于M、N两点,直线MA、NA与直线



正确答案
见解析
解析
(1)设

又
故

(2)设直线MN的方程为
设
直线MA的方程为


得
所以
所以


故直线l的方程为
知识点
如图,已知⊙O是



(1)求证:
(2)过点




正确答案
见解析
解析
(1)证明:连结

所以

则

又

(2)因为

又

因为

则

知识点
过椭圆






正确答案
答案:
解析
由题意知点P的坐标为(-c,



知识点
已知直线l:y=2x-2与抛物线M:y=x2的切线m平行
(1)求切线m的方程和切点A的坐标
(2)若点P是直线l上的一个动点,过点P作抛物线M的两条切线,切点分别为B,C,同时分别与切线m交于点E,F试问
正确答案
见解析
解析
解:(1)设切点




(2)设

∵
∴切线


联立方程组

∵点



又∵直线
∴点

又由
∴
∴
又由联立方程组

∴
∴
知识点
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD。
(1)求证:AB∥EF;
(2)求证:平面BCF⊥平面CDEF;
(3)若




正确答案
见解析
解析
(1)因为四边形ABCD是矩形,所以AB∥CD,
因为

所以AB∥平面CDEF,……………………… 4分
因为


所以AB∥EF。
(2)因为DE⊥平面ABCD,
所以DE⊥BC。
因为BC⊥CD,

所以BC⊥平面CDEF。
因为BC
(3)方法一:点E到平面MBD的距离转化为点B到平面MED的距离=
方法二:以D为原点,DA为x轴,DC为y轴,DE为z轴,建系计算得距离=
知识点
在△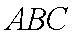
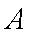
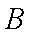
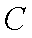
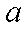
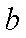

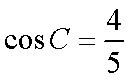
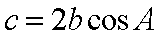
(1)求证: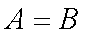
(2)若△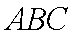
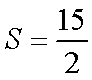

正确答案
见解析
解析
(1)证明:因为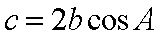
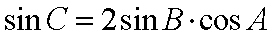
所以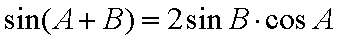
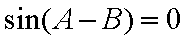
在△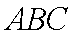
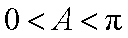
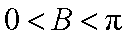
所以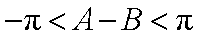
即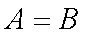
(2)解:由(1)知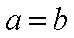
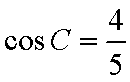
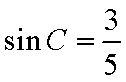
因为△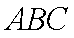
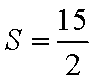
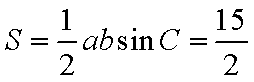
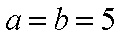
由余弦定理
所以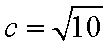
知识点
扫码查看完整答案与解析