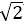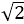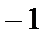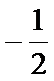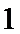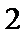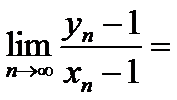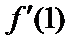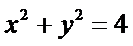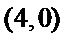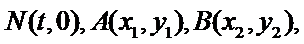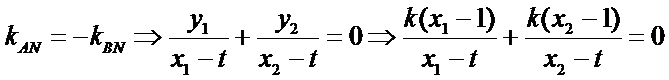- 直线和圆的方程
- 共1163题
8.若直线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知圆
(1)若


(2)是否存在






正确答案
(1)由圆方程配方得(x+1)2+(y-3)2=9,
圆心为C(-1,3),
半径为 r = 3,
若 l与C相切,
则得
∴(3m-4)2=9(1+m2),
∴m =
(2)假设存在m满足题意。
由
(m2+1)y2-(8m+6)y+16=0,
由△=(8m+6)2-4(m2+1)·16>0,
得m>
设A(x1,y1),B(x2,y2),
则y1+y2=


=(3-my1)(3-my2)+y1y2
=9-3m(y1+y2)+(m2+1)y1y2
=9-3m·
=25-
24m2+18m=25m2+25,m2-18m+25=0,
∴m=9±2

∴存在m=9±2
解析
解析已在路上飞奔,马上就到!
知识点
5.直线l过点(

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知椭圆E:
(1)求圆C的方程;
(2)若直线FG与直线l交于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(3)在平面上是否存在定点P, 使得
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.过点(

正确答案
解析
如图,
∵S△AOB=


当∠AOB=
此时点O到AB的距离d=
设AB的方程为y=k(x-

由d=


知识点
3.直线y=kx+3与圆(x-


正确答案
解析
如图,设圆的圆心为C(
作CD⊥MN于点D,则|CD|=


即



知识点
4.已知圆面C:(x-a)2+y2≤a2-1的面积为S,平面区域D:2x+y≤4与圆面C的公共区域的面积大于
正确答案
解析
依题意并结合图形(图略)分析可知
圆面C:(x-a)2+y2≤a2-1的圆心(a,0)应在不等式2x+y≤4表示的平面区域内
则有
因此实数a的取值范围是(-∞,-1)∪(1,2).
知识点
5.若圆C:(x-2a)2+(y-a)2=(a+1)2与两个坐标轴均有公共点,则实数a的取值范围是( )
正确答案
解析
要圆C与两个坐标轴均有公共点,只需要圆心到两个坐标轴的距离小于等于或半径,
即

知识点
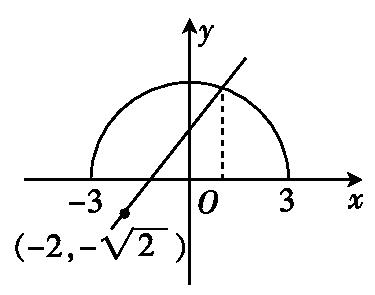
16.若不等式
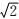
正确答案
解析
令y1=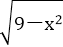
其中-3≤x≤3,在同一个坐标系中作出y1,y2的图象,如图所示.
由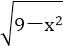
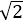
结合图象知b=3,a=1,即直线y2与圆y1的交点坐标为(1,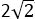
又因为点(-2,-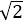
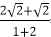
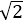
知识点
20.如图,


(1)求点M的轨迹C的方程;
(2)过点

正确答案
解:(1)设点



则



因为


将①代入②,得点

(2)由题意知,
当


此时


当

由
得
设A、B两点的坐标分别为

又由l与圆

所以
因为

所以|AB|的最大值为2
依题意,圆心

所以

当且仅当

解析
解析已在路上飞奔,马上就到!
知识点
18.设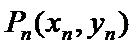
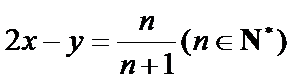
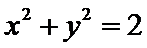
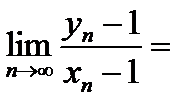
正确答案
解析
当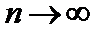
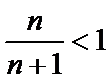
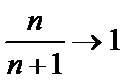
而由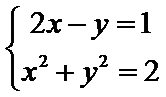
所以
而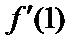
又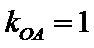
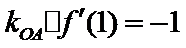
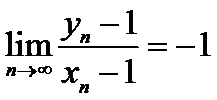
故选A.
知识点
14. 已知过点



正确答案
【答案】x-3y-6=0 ,
解析
由已知可得圆的半径为5,而弦长刚好等于直径,所以直线经过圆心,由直线方程的两点式方程可以求出直线的方程为x-3y-6=0。
考查方向
解题思路
本题可以将已知条件转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去利用勾股定理算出圆心到直线的距离,然后利用点到直线的距离构造一个关于斜率的方程解出即可。
易错点
本题不知道将已知转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去求解。
知识点
20.已知点M(-1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N距离的
(Ⅰ)求曲线E的方程;
(Ⅱ)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点.若CD的斜率为-1,求直线CD的方程.
正确答案
(1)
(2)y=-x,或y=-x+3.
解析
(1)直接按照步骤来求
(2)要注意对参数的讨论.
⑴解:设曲线

由题意,
整理得

⑵解:由题知

设曲线


线段



设直线

由

由圆的几何性质,





所以直线


考查方向
本题考查了圆的标准方程和直线与圆的位置关系,属于高考中的高频考点.
解题思路
解题步骤如下:
1、利用已知求解。
2、联立直线与圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
20.已知直线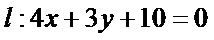
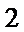
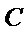
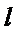
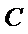
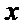
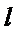
(Ⅰ)求圆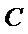
(Ⅱ)过点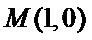
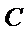
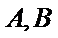
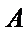
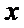
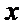
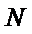
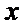
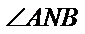
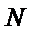
正确答案
(Ⅰ)
(Ⅱ)存在N
解析
试题分析:本题是直线与圆的位置关系的常见题型,运算量较大。此类问题往往要用到韦达定理,设而不求等方法技巧,把几何关系转化为代数运算。
(Ⅰ)设圆心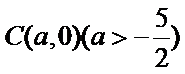
则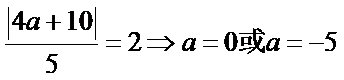
所以圆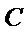
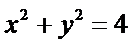
(Ⅱ)当直线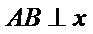
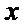
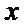
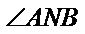
当直线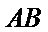
设直线
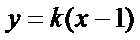
联立圆
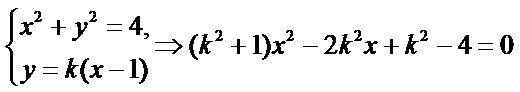
故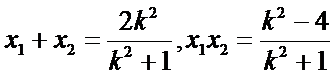
若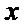
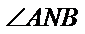
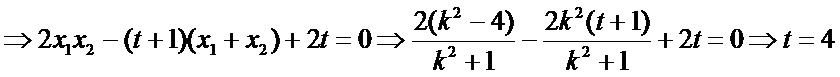
当点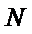
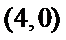
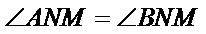
考查方向
解题思路
本题主要考查圆的标准方程、直线与圆的位置关系、点到直线的距离公式等基础知识,
解题步骤如下:根据直线与圆相切的定义,求出圆方程;由直线与圆的位置关系,建立方程组,结合韦达定理,和斜率关系,得出结果。
易错点
第一问易忽视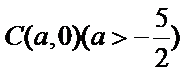
第二问不能理解“若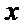
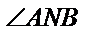
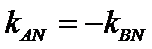
知识点
扫码查看完整答案与解析