- 推理与证明
- 共78题
回答下列问题。
36.求
37.设


正确答案
0
解析

考查方向
解题思路
根据组合数公式化简求值
易错点
组合数公式,错位相减求和,组合数性质的应用。
正确答案
对任意的
① 当


② 假设
即
当
左=

右边
而
因此
因此左边=右边,
因此
综合①②可得命题对任意
另解:因为
左边
又由

所以,左边
解析
对任意的
① 当


② 假设
即
当
左=

右边
而
因此
因此左边=右边,
因此
综合①②可得命题对任意
另解:因为
左边
又由

所以,左边
考查方向
解题思路
设置目的指向应用组合数性质解决问题,而组合数性质不仅有课本上的




易错点
组合数公式,错位相减求和,组合数性质的应用。
13.已知










正确答案
71
解析
解析已在路上飞奔,马上就到!
知识点
14.求“方程5x+12x=13x的解”有如下解题思路:设f(x)= 

正确答案
x=-1或x=1
解析
类比上述解题思路,设f(x)=x3+x,由于f'(x)=3x2+1≥0,则f(x)在R上单调递增,∵x3+x=

知识点
14.求“方程5x+12x=13x的解”有如下解题思路:设f(x)= 

正确答案
x=-1或x=1
解析
类比上述解题思路,设f(x)=x3+x,由于f'(x)=3x2+1≥0,则f(x)在R上单调递增,∵x3+x=

知识点
13.原对大于或等于


根据上述分解规律,

正确答案
31+33+35+37+39+41
解析
解析已在路上飞奔,马上就到!
知识点
3.下列函数中,满足
正确答案
解析
根据选项代入数值,依次判断,可知,此题选C
考查方向
1.抽象函数;2.函数单调性.
解题思路
根据函数单调性的性质,结合选项依次判断
易错点
对函数性质不了解
知识点
7.已知集合


得





其中是“
正确答案
解析
易知(1,0)∈M,但不存在(0,y)∈M,故①不正确;
故排除C,D;设(x1,y1)∈M,(x2,y2)∈M,
则
由基本不等式可知:最小值为2,所以“3”不正确,故排除A,所以选B
考查方向
集合的表示法
新定义的集合的特征
解题思路
观察选项,利用排除法确定答案
易错点
对新定义的性质掌握不好,基本不等式掌握不牢固
知识点
11.《算数书》是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也. 又以高乘之,三十六成一. 该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式



正确答案
解析
设圆锥底面圆的半径为
所以
考查方向
圆锥体积的计算
解题思路
先表示出圆锥的体积,然后反求
易错点
公式记忆不准确,化简错误
知识点
若数列{an}是各项均为正数的等比数列,则当
正确答案
解析
由条件类比可知:dn=
数列{dn}也是等差数列。
知识点
13.公比为4的等比数列











正确答案
300
解析
解析已在路上飞奔,马上就到!
知识点
若式子






正确答案
解析
略
知识点
设















正确答案
解析
略
知识点
如图,设

组成的集合记为M,如果集合M中有且只有2个元素,那么符合条件的点P有( )
正确答案
解析
略
知识点
设集合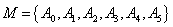
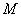
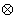
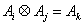
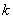
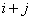
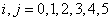
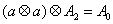
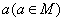
正确答案
解析
设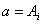
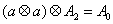
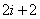
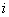
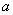
知识点
对任意实数







正确答案
解析
略
知识点
扫码查看完整答案与解析