基本不等式的实际应用
共15题

· 基本不等式的实际应用

基本不等式的实际应用
共15题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

某工厂生产某种产品，每日的成本C（单位：元）与日产里x（单位：吨）满足函数关系式C=3+x，每日的销售额R（单位：元）与日产量x满足函数关系式，已知每日的利润L=S﹣C，且当x=2时，L=3

（1）求k的值；

（2）当日产量为多少吨时，毎日的利润可以达到最大，并求出最大值。

正确答案

见解析。

解析

解：（1）由题意可得：L=

因为x=2时，L=3

所以3=2×2++2

所以k=18

（2）当0＜x＜6时，L=2x++2

所以L=2（x﹣8）++18=﹣[2（8﹣x）+]+18≤﹣2+18=6

当且仅当2（8﹣x）=即x=5时取等号

当x≥6时，L=11﹣x≤5

所以当x=5时，L取得最大值6

所以当日产量为5吨时，毎日的利润可以达到最大值6。

知识点

函数模型的选择与应用基本不等式的实际应用

题型：填空题

填空题 · 5 分

设变量满足，则的取值范围是 .

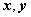
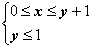
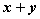
正确答案

解析

略

知识点

基本不等式的实际应用

题型：简答题

简答题 · 12 分

设等差数列｛｝的前n项和为，且, 。

（1）求数列｛｝的通项公式；

（2）设数列｛｝的前n项和，且（为常数），令.求数列｛｝的前n项和。

正确答案

（1）

（2）

解析

(1)解:设等差数列{}的首项为,公差为,

因为已知,

可得,即

整理得， ①

又因为,

当时，

即， ②

①②联立可得

由于

所以，.

(2)解:由(Ⅰ)可得，且

将带入，可得

①

当时，

当时，②

①-②可得

所以

两式相减得

所以

知识点

基本不等式的实际应用

题型：单选题

单选题 · 5 分

已知两条直线和，与函数的图像从左至右相交于点，与函数的图像从左至右相交于点，记线段AC和BD在轴上的投影长度分别为，当m变化时，的最小值为

正确答案

解析

在同一坐标系中作出y=m，y=(m＞0)，图像如下图，

由= m，得，= ，得.

依照题意得.

，.

知识点

利用基本不等式求最值基本不等式的实际应用

题型：简答题

简答题 · 14 分

已知数列满足a=1,(n∈N)

（1）若数列满足(n∈N*),证明: 是等差数列;

（2）证明:(n∈N*)。

正确答案

见解析

解析

（1）解：

是以为首项，2为公比的等比数列。

证法一：，

　　　　　　　　　　　　　①

　　　　　②

②－①，得即

③－④，得　

即　

是等差数列。

证法二：同证法一，得

令得

设下面用数学归纳法证明　

（1）当时，等式成立。

（2）假设当时，那么

这就是说，当时，等式也成立。

根据（1）和（2），可知对任何都成立。

是等差数列。

（2）证明：

知识点

基本不等式的实际应用

继续学习学习下一知识点

下一知识点 : 不等式的实际应用

百度题库 > 高考 > 理科数学 > 基本不等式的实际应用

扫码查看完整答案与解析